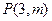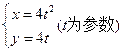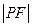题目内容
AB是过抛物线y2=2x的焦点F的弦，且|AB|=4，则AB的中点C到直线x+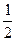
=0的距离为________________.
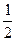=0的距离为________________.2
如图所示，直线x+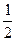=0是抛物线y2=2x的准线.
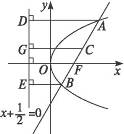
过A、B、C分别作直线x+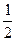=0的垂线，垂足为D、E、G.
由抛物线定义得|BF|=|BE|，|AF|=|AD|.
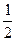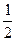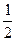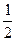∴|CG|=（|AD|+|BE|）=（|AF|+|BF|）=|AB|=×4=2.
∴C到直线x+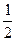=0的距离为2.
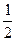=0是抛物线y2=2x的准线.过A、B、C分别作直线x+
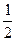=0的垂线，垂足为D、E、G.由抛物线定义得|BF|=|BE|，|AF|=|AD|.
∴|CG|=
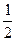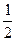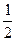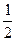（|AD|+|BE|）=（|AF|+|BF|）=|AB|=×4=2.∴C到直线x+
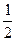=0的距离为2.
练习册系列答案
相关题目
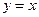对称，则C2的准线方程是 .
