题目内容
已知抛物线y2=2px(p>0)过动点M(a,0)且斜率为1的直线l与该抛物线交于不同的两点A、B,|AB|≤2p.
(1)求实数a的取值范围;
(2)若线段AB的垂直平分线交x轴于点N,求△NAB面积的最大值.
(1)求实数a的取值范围;
(2)若线段AB的垂直平分线交x轴于点N,求△NAB面积的最大值.
(1)∴-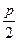 <a≤-
<a≤-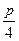 .
.
(2)△NBA的面积最大值为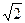 p2.
p2.
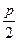 <a≤-
<a≤-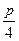 .
.(2)△NBA的面积最大值为
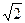 p2.
p2.(1)设直线l:y=x-a,
由 x2-2ax+a2-2px=0,
x2-2ax+a2-2px=0,
即x2-(2a+2p)x+a2=0.设A(x1,y1)、B(x2,y2),则
则|AB|=
= ≤2p.
≤2p.
∴0<8p(p+2a)≤4p2.
又∵p>0,∴-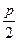 <a≤-
<a≤-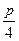 .
.
(2)设AB的垂直平分线交AB于点Q,令Q(x0,y0),
则
∴|QM|2=(a+p-a)2+(p-0)2=2p2.
又△MNQ为等腰直角三角形,
∴|QN|=|QM|=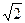 p.
p.
∴S△NAB=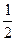 |AB|·|QN|=
|AB|·|QN|= p·|AB|≤
p·|AB|≤ p·2p=
p·2p=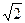 p2,
p2,
即△NBA的面积最大值为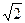 p2.
p2.
由
 x2-2ax+a2-2px=0,
x2-2ax+a2-2px=0,即x2-(2a+2p)x+a2=0.设A(x1,y1)、B(x2,y2),则

则|AB|=

=
 ≤2p.
≤2p.∴0<8p(p+2a)≤4p2.
又∵p>0,∴-
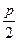 <a≤-
<a≤-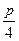 .
.(2)设AB的垂直平分线交AB于点Q,令Q(x0,y0),
则

∴|QM|2=(a+p-a)2+(p-0)2=2p2.
又△MNQ为等腰直角三角形,
∴|QN|=|QM|=
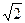 p.
p.∴S△NAB=
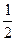 |AB|·|QN|=
|AB|·|QN|= p·|AB|≤
p·|AB|≤ p·2p=
p·2p=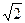 p2,
p2,即△NBA的面积最大值为
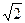 p2.
p2.
练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
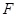 为抛物线
为抛物线 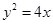 的焦点,
的焦点,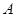 、
、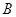 、
、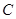 为该抛物线上三点,若
为该抛物线上三点,若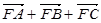 =0,则
=0,则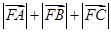 的值为
的值为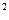 =4x的焦点,作直线与此抛物线相交于两点P和Q,那么线段PQ中点的轨迹方程是( )
=4x的焦点,作直线与此抛物线相交于两点P和Q,那么线段PQ中点的轨迹方程是( )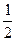 =0的距离为________________.
=0的距离为________________.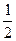 ,则实数m的值为________________.
,则实数m的值为________________.