题目内容
已知经过点A(-4,0)的动直线l与抛物线G: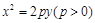 相交于B、C,当直线l的斜率是
相交于B、C,当直线l的斜率是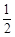 时,
时,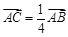 .
.
(Ⅰ)求抛物线G的方程;
(Ⅱ)设线段BC的垂直平分线在y轴上的截距为b,求b的取值范围.
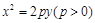 相交于B、C,当直线l的斜率是
相交于B、C,当直线l的斜率是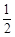 时,
时,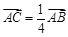 .
.(Ⅰ)求抛物线G的方程;
(Ⅱ)设线段BC的垂直平分线在y轴上的截距为b,求b的取值范围.
(Ⅰ)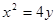 ;(Ⅱ)
;(Ⅱ)
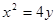 ;(Ⅱ)
;(Ⅱ)
试题分析:该题考察抛物线的方程、韦达定理、直线和抛物线的位置关系、向量等基础知识,考察数形结合、综合分析和解决问题能力、基本运算能力,(Ⅰ)求直线
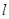 的方程:
的方程: ,和抛物线
,和抛物线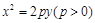 联立,得
联立,得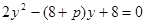
设
 ,代入 向量式
,代入 向量式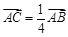 中,得
中,得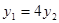 ,然后联立
,然后联立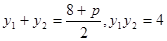
可得
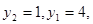 ∴
∴ ,∴抛物线方程为
,∴抛物线方程为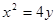 ;(Ⅱ)设直线
;(Ⅱ)设直线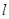 的方程:
的方程: ,
, ,线段
,线段 的中点
的中点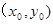 ,将
,将 与
与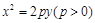 联立,可得
联立,可得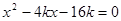 ,因为直线与抛物线交与两点
,因为直线与抛物线交与两点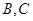 ,所以
,所以 ,可得
,可得 或
或 ,再表示中点
,再表示中点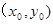 ,进而可求线段
,进而可求线段 的中垂线方程,令
的中垂线方程,令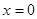 ,可得其在
,可得其在 轴的截距
轴的截距 ,求其值域即可.
,求其值域即可.试题解析:(1)设
 ,由已知k1=
,由已知k1=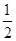 时,l方程为
时,l方程为
即x=2y-4.
由
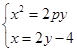 得
得
∴
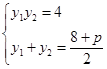
又∵

∴
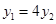 5分
5分由p>0得
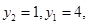 ∴
∴ ,即抛物线方程为:
,即抛物线方程为: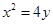 .
.(2)设l:
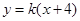 ,BC中点坐标为
,BC中点坐标为
由
 得:
得: ①
①∴x0=
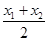 =2k,y0=k(x0+4)=2k2+4k.
=2k,y0=k(x0+4)=2k2+4k.∴BC的中垂线方程为y?2k2?4k=?
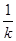 (x?2k)
(x?2k)∴BC的中垂线在y轴上的截距为:b=2k2+4k+2=2(k+1)2
对于方程①由△=16k2+64k>0得:
 或
或 .
.∴
 12分
12分

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
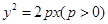 的焦点为
的焦点为 ,其准线与
,其准线与 轴的交点为
轴的交点为 ,过
,过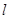 交抛物线于
交抛物线于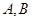 两点.
两点.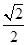 ,求证:
,求证: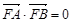 ;
;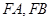 的斜率分别为
的斜率分别为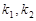 ,求
,求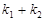 的值.
的值.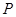 :
: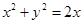 及抛物线
及抛物线 :
: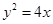 ,过圆心
,过圆心 ,此直线与上述两曲线的四个交点,自上而下顺次记为
,此直线与上述两曲线的四个交点,自上而下顺次记为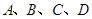 ,如果线段
,如果线段 的长按此顺序构成一个等差数列,求直线
的长按此顺序构成一个等差数列,求直线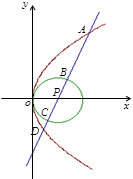
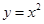 上,A,C关于
上,A,C关于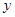 轴对称,BD平行于抛物线在点C处的切线。
轴对称,BD平行于抛物线在点C处的切线。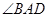 ;
;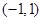 ,四边形ABCD的面积为4,求直线BD的方程。
,四边形ABCD的面积为4,求直线BD的方程。 上与焦点的距离等于6的点横坐标是( )
上与焦点的距离等于6的点横坐标是( ) 的焦点坐标为 .
的焦点坐标为 .  与抛物线
与抛物线 有一个公共的焦点,且双曲线上的点到坐标原点的最短距离为1,则该双曲线的标准方程是___________。
有一个公共的焦点,且双曲线上的点到坐标原点的最短距离为1,则该双曲线的标准方程是___________。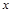 轴上一点
轴上一点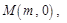 抛物线
抛物线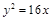 上任意一点
上任意一点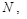 满足
满足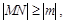 则
则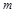 的取值范围是( )
的取值范围是( )