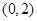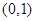题目内容
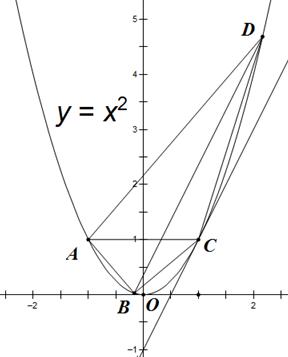
四边形ABCD的四个顶点都在抛物线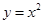 上,A,C关于
上,A,C关于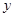 轴对称,BD平行于抛物线在点C处的切线。
轴对称,BD平行于抛物线在点C处的切线。
(Ⅰ)证明:AC平分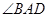 ;
;
(Ⅱ)若点A坐标为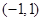 ,四边形ABCD的面积为4,求直线BD的方程。
,四边形ABCD的面积为4,求直线BD的方程。
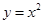 上,A,C关于
上,A,C关于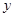 轴对称,BD平行于抛物线在点C处的切线。
轴对称,BD平行于抛物线在点C处的切线。(Ⅰ)证明:AC平分
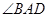 ;
;(Ⅱ)若点A坐标为
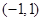 ,四边形ABCD的面积为4,求直线BD的方程。
,四边形ABCD的面积为4,求直线BD的方程。(Ⅰ)详见解析;(Ⅱ)y=2x
试题分析:(Ⅰ)依题意设出A、B、C、D四点的坐标,注意到AC的斜率为0,只需证AB、AD的斜率之和为0即可;(Ⅱ)四边形ABCD可以AC为底分成两个三角形求出面积,解出得到的方程即可.
试题解析:(Ⅰ)设A(x0,
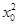 ),B(x1,
),B(x1, ),C(-x0,
),C(-x0,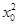 ),D(x2,
),D(x2, ).
).对y=x2求导,得y¢=2x,则抛物线在点C处的切线斜率为-2x0.
直线BD的斜率k=
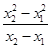 =x1+x2,
=x1+x2,依题意,有x1+x2=-2x0.
记直线AB,AD的斜率分别为k1,k2,与BD的斜率求法同理,得
k1+k2=(x0+x1)+(x0+x2)=2x0+(x1+x2)=0,
所以∠CAB=∠CAD,即AC平分∠BAD.
(Ⅱ)由题设,x0=-1,x1+x2=2,k=2.四边形ABCD的面积
S=
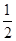 |AC|·
|AC|·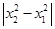 =
=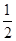 |AC|·|x2+x1|·|x2-x1|
|AC|·|x2+x1|·|x2-x1|=
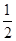 ×2×2×|2-2x1|=4|1-x1|,
×2×2×|2-2x1|=4|1-x1|,由已知,4|1-x1|=4,得x1=0,或x1=2.
所以点B和D的坐标为(0,0)和(2,4),
故直线BD的方程为y=2x.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
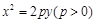 相交于B、C,当直线l的斜率是
相交于B、C,当直线l的斜率是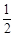 时,
时,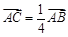 .
. ,且在x轴上截得弦长为2,记该圆圆心的轨迹为E.
,且在x轴上截得弦长为2,记该圆圆心的轨迹为E. 的直线m交曲线E于A,B两点,过A,B两点分别作曲线E的切线,两切线交于点C,当△ABC的面积为
的直线m交曲线E于A,B两点,过A,B两点分别作曲线E的切线,两切线交于点C,当△ABC的面积为 时,求直线m的方程.
时,求直线m的方程.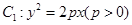 的焦点
的焦点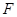 以及椭圆
以及椭圆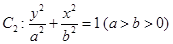 的上、下焦点及左、右顶点均在圆
的上、下焦点及左、右顶点均在圆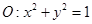 上.
上.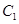 和椭圆
和椭圆 的标准方程;
的标准方程;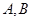 两不同点,交
两不同点,交 轴于点
轴于点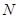 ,已知
,已知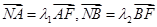 ,求
,求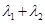 的值;
的值;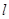 交椭圆
交椭圆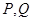 两不同点,
两不同点,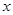 轴的射影分别为
轴的射影分别为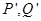 ,
,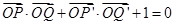 ,若点
,若点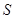 满足
满足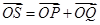 ,证明:点
,证明:点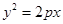
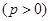 ,过其焦点且斜率为-1的直线交抛物线于
,过其焦点且斜率为-1的直线交抛物线于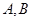 两点,若线段
两点,若线段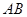 的中点的横坐标为3,则该抛物线的准线方程为( )
的中点的横坐标为3,则该抛物线的准线方程为( )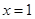
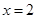
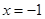
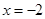
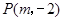 到焦点的距离为4,则
到焦点的距离为4,则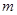 的值为( )
的值为( )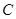 :
: 上有一点
上有一点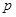 ,若它到点
,若它到点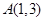 的距离与它到抛物线
的距离与它到抛物线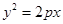 的焦点
的焦点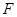 与双曲线
与双曲线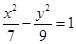 的右焦点重合,抛物线的准线与
的右焦点重合,抛物线的准线与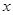 轴的交点为
轴的交点为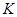 ,点
,点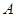 在抛物线上且
在抛物线上且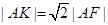 ,则△
,则△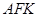 的面积为 .
的面积为 .  的焦点是
的焦点是