题目内容
【题目】已知椭圆![]() 的长轴是短轴的两倍,以短轴一个顶点和长轴一个顶点为端点的线段作直径的圆的周长等于
的长轴是短轴的两倍,以短轴一个顶点和长轴一个顶点为端点的线段作直径的圆的周长等于![]() ,直线l与椭圆C交于
,直线l与椭圆C交于![]() 两点.
两点.
(1)求椭圆C的方程;
(2)过点O作直线l的垂线,垂足为D.若![]() ,求动点D的轨迹方程.
,求动点D的轨迹方程.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)由题意知![]() ,
,![]() ,即可求得椭圆方程;(2)先考虑直线斜率存在时,设直线的方程为
,即可求得椭圆方程;(2)先考虑直线斜率存在时,设直线的方程为![]() ,与椭圆方程联立,结合向量的垂直关系即可求得m,k的关系式,从而求得
,与椭圆方程联立,结合向量的垂直关系即可求得m,k的关系式,从而求得![]() ,再验证斜率不存在时也满足,则可求得点D的轨迹方程.
,再验证斜率不存在时也满足,则可求得点D的轨迹方程.
(1)由题意知,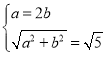 ,解得
,解得![]() ,所以椭圆C的方程为
,所以椭圆C的方程为![]()
(2)当直线l的斜率存在时,设直线l的方程为![]() ,
,
由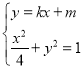 消去y整理得
消去y整理得![]() ,根据题设有:
,根据题设有:
![]() 且
且![]() ,
,![]() .
.
∵![]() ,∴
,∴![]() ,即
,即![]() ,
,
将![]() ,
,![]() 代入,化得
代入,化得![]() ,
,
把![]() ,
,![]() 代入整理得:
代入整理得:![]() ,
,
∵![]() ,∴
,∴ ;
;
当直线l的斜率不存在时,设![]() ,由
,由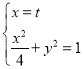 得
得![]() ,
,![]() .
.
∵![]() ,∴
,∴![]() ,解得
,解得![]() ,∴
,∴![]()
所以动点D的轨迹是以原点O为圆心,半径为![]() 的圆,方程为
的圆,方程为![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某学校数学建模小组为了研究双层玻璃窗户中每层玻璃厚度![]() (每层玻璃的厚度相同)及两层玻璃间夹空气层厚度
(每层玻璃的厚度相同)及两层玻璃间夹空气层厚度![]() 对保温效果的影响,利用热传导定律得到热传导量
对保温效果的影响,利用热传导定律得到热传导量![]() 满足关系式:
满足关系式: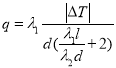 ,其中玻璃的热传导系数
,其中玻璃的热传导系数![]() 焦耳/(厘米
焦耳/(厘米![]() 度),不流通、干燥空气的热传导系数
度),不流通、干燥空气的热传导系数![]() 焦耳/(厘米
焦耳/(厘米![]() 度),
度), ![]() 为室内外温度差.
为室内外温度差.![]() 值越小,保温效果越好.现有4种型号的双层玻璃窗户,具体数据如下表:
值越小,保温效果越好.现有4种型号的双层玻璃窗户,具体数据如下表:
型号 | 每层玻璃厚度 (单位:厘米) | 玻璃间夹空气层厚度 (单位:厘米) |
A型 |
|
|
B型 |
|
|
C型 |
|
|
D型 |
|
|
则保温效果最好的双层玻璃的型号是________型.