Question

【题目】已知函数．

（1）若，，求的值域；

（2）当时，求的最小值；

（3）是否存在实数、，同时满足下列条件：① ；② 当的定义域为时，其值域为．若存在，求出、的值；若不存在，请说明理由．

Answer 1

【答案】(1) (2) 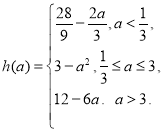(3) 不存在满足条件的实数、．见解析

【解析】

（1）设t＝3x，则φ（t）＝t2﹣2at+3＝（t﹣a）2+3﹣a2，φ（t）的对称轴为t＝a，当a＝1时，即可求出f（x）的值域；

（2）由函数φ（t）的对称轴为t＝a，分类讨论当a时，当a≤3时，当a＞3时，求出最小值，则h（a）的表达式可求；

（3）假设满足题意的m，n存在，函数h（a）在（3，+∞）上是减函数，求出h（a）的定义域，值域，然后列出不等式组，求解与已知矛盾，即可得到结论．

（1）当时，由，得，

因为，所以，．

（2）令，因为，故，函数可化为

．

① 当时，；

② 当时，；

③ 当时，．

综上，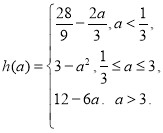

（3）因为，为减函数，

所以在上的值域为，

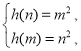又在上的值域为，所以， 即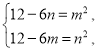

两式相减，得，

因为，所以，而由可得，矛盾．

所以，不存在满足条件的实数、．