题目内容
【题目】已知数列{an}的首项a1＝1，an＋1＝
(n∈N*)．
(1)证明：数列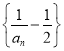
是等比数列；
(2)设bn＝
，求数列{bn}的前n项和Sn.
【答案】（1）见解析（2）
【解析】试题分析:（1）根据等比数列定义，代入条件化简即得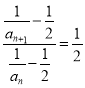
（2）先求出
，再利用分组求和以及错位相减法得数列{bn}的前n项和Sn.
试题解析：解：(1)证明：∵an＋1＝
，∴
＝
＝
＋
.
∴－
＝
.又∵a1＝1，∴
－＝，
∴数列
是以为首项，为公比的等比数列．
(2)解：由(1)知
－＝·
n－1＝
，
即＝＋，∴bn＝
＝
＋
.
设Tn＝＋
＋
＋…＋，①
则Tn＝
＋
＋…＋
＋
，②
①－②，得Tn＝＋＋…＋－＝1－－，
∴Tn＝2－
－.
又∵ (1＋2＋3＋…＋n)＝
，
∴数列{bn}的前n项和Sn＝2－
＋
.
【题目】如图，在等腰梯形
中， 
，上底
，下底
，点
为下底
的中点，现将该梯形中的三角形
沿线段
折起，形成四棱锥
.
（1）在四棱锥
中，求证： 
；
（2）若平面
与平面
所成二面角的平面角为
，求直线
与平面
所成角的正弦值.
【题目】甲、乙两家外卖公司，其送餐员的日工资方案如下：甲公司的底薪70元，每单抽成3元；乙公司无底薪，40单以内（含40单）的部分每单抽成5元，超出40单的部分每单抽成7元，假设同一公司送餐员一天的送餐单数相同，现从两家公司各随机抽取一名送餐员，并分别记录其100天的送餐单数，得到频数表如下：
甲公司送餐员送餐单数频数表
送餐单数 | 38 | 39 | 40 | 41 | 42 |
天数 | 20 | 40 | 20 | 10 | 10 |
乙公司送餐员送餐单数频数表
送餐单数 | 38 | 39 | 40 | 41 | 42 |
天数 | 10 | 20 | 20 | 40 | 10 |
将上表中的频率视为概率，回答下列问题：
（1）现从甲公司随机抽取3名送餐员，求恰有2名送餐员送餐单数超过40的概率；
（2）（i）记乙公司送餐员日工资为X（单位：元），求X的数学期望；
（ii）某人拟到甲、乙两家公司中的一家应聘送餐员，如果仅从日平均工资的角度考虑，他应该选择去哪家公司应聘，说明理由．