题目内容
如图,四棱锥 的底面
的底面 为一直角梯形,侧面PAD是等边三角形,其中
为一直角梯形,侧面PAD是等边三角形,其中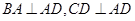 ,
, ,平面
,平面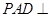 底面
底面 ,
, 是
是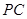 的中点.
的中点.

(1)求证: //平面
//平面 ;
;
(2)求证: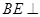
 ;
;
(3)求 与平面
与平面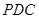 所成角的正弦值。
所成角的正弦值。
 的底面
的底面 为一直角梯形,侧面PAD是等边三角形,其中
为一直角梯形,侧面PAD是等边三角形,其中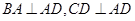 ,
, ,平面
,平面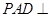 底面
底面 ,
, 是
是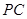 的中点.
的中点.
(1)求证:
 //平面
//平面 ;
;(2)求证:
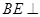
 ;
;(3)求
 与平面
与平面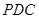 所成角的正弦值。
所成角的正弦值。(1)详见解析(2)详见解析(3)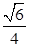 .
.
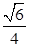 .
.试题分析:(1)证BE∥平面PAD,可先构建平面EBM,证明平面EBM∥平面APD,由面面平行,得到线面平行;
(2)取PD的中点F,连接FE,根据线面垂直的判定及性质,及等腰三角形性质,结合线面垂直的判定定理可得AF⊥平面PDC,又由BE∥AF,可得BE⊥平面PDC;
(3)证明AF⊥平面PCD,连接DE,则∠BDE为BD与平面PDC所成角..
试题解析:(1)证明:如图,
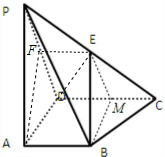
取CD的中点M,连接EM、BM,则四边形ABMD为矩形
∴EM∥PD,BM∥AD;
又∵BM∩EM=M,
∴平面EBM∥平面APD;
而BE?平面EBM,
∴BE∥平面PAD;
(2)证明:取PD的中点F,连接FE,则FE∥DC,BE∥AF,
又∵DC⊥AD,DC⊥PA,
∴DC⊥平面PAD,
∴DC⊥AF,DC⊥PD,
∴EF⊥AF,
在Rt△PAD中,∵AD=AP,F为PD的中点,
∴AF⊥PD,又AF⊥EF且PD∩EF=F,
∴AF⊥平面PDC,又BE∥AF,
∴BE⊥平面PDC,
∴CD⊥BE;
(3)解:∵CD⊥AF,AF⊥PD,CD∩PD=D,
∴AF⊥平面PCD,
连接DE,则∠BDE为BD与平面PDC所成角.
在直角△BDE中,设AD=AB=a,则BE=AF=
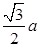 ,BD=
,BD=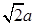 ,∴sin∠BDE=
,∴sin∠BDE=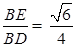 .
.
练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案
相关题目
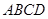 是边长为2的正方形,
是边长为2的正方形,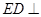 平面
平面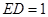 ,
,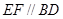 ,且
,且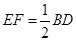 .
.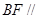 平面
平面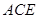 ;
;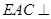 平面
平面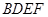 ;
;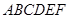 的体积。
的体积。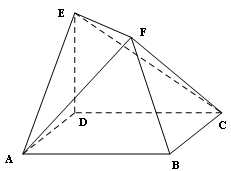
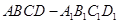 中,
中,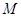 是
是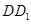 的中点.
的中点. 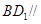 平面
平面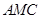 ;
;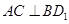 ;
;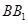 上是否存在点
上是否存在点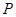 ,当
,当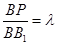 时,平面
时,平面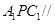 平面
平面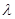 的值并证明;若不存在,请说明理由.
的值并证明;若不存在,请说明理由.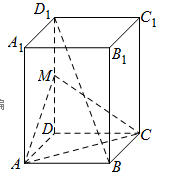
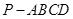 中,底面
中,底面 为平行四边形,
为平行四边形, ,
, ,
,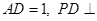 底面
底面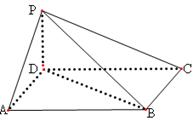
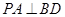 ;
;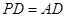 ,求二面角
,求二面角 余弦值.
余弦值. 的底面是边长为1的正方形,
的底面是边长为1的正方形,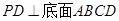 ,点E在棱PB上.
,点E在棱PB上.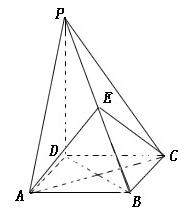
 ;
;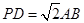 且E为PB的中点时,求AE与平面PDB
且E为PB的中点时,求AE与平面PDB
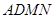 都为正方形,
都为正方形,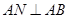 ,F
,F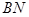 的中点,E为线段BC上的动点.
的中点,E为线段BC上的动点.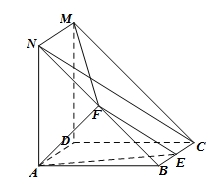
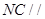 平面AEF;
平面AEF;
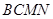 平面;
平面;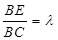 ,写出
,写出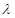 为何值时MF⊥平面AEF(结论不要求证明).
为何值时MF⊥平面AEF(结论不要求证明).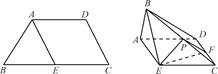
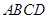 沿对角线
沿对角线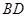 折成直二面角
折成直二面角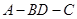 ,有如下四个结论:
,有如下四个结论: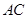 ⊥
⊥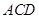 是等边三角形;③
是等边三角形;③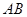 与平面
与平面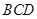 所成的角为60°;
所成的角为60°;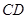 所成的角为60°.其中错误的结论是
所成的角为60°.其中错误的结论是