题目内容
如图①,在等腰梯形ABCD中,AD∥BC,AB=AD,∠ABC=60°,E是BC的中点.如图②,将△ABE沿AE折起,使二面角BAEC成直二面角,连结BC、BD,F是CD的中点,P是棱BC的中点.求证:
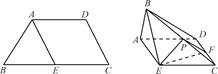
图①图②
(1)AE⊥BD;
(2)平面PEF⊥平面AECD.

图①图②
(1)AE⊥BD;
(2)平面PEF⊥平面AECD.
(1)见解析(2)见解析
(1)取AE中点M,连结BM、DM、DE.
∵在等腰梯形ABCD中,AD∥BC,AB=AD,∠ABC=60°,E是BC的中点,∴△ABE与△ADE都是等边三角形,∴BM⊥AE,DM⊥AE.∵BM∩DM=M,BM,DM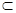 平面BDM,∴AE⊥平面BDM.∵BD
平面BDM,∴AE⊥平面BDM.∵BD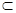 平面BDM,∴AE⊥BD.
平面BDM,∴AE⊥BD.
(2)连结CM交EF于点N,连结PN.
∵ME∥FC,且ME=FC,∴四边形MECF是平行四边形,∴N是线段CM的中点.∵P是线段BC的中点,∴PN∥BM.∵BM⊥平面AECD,∴PN⊥平面AECD.∵PN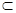 平面PEF,∴平面PEF⊥平面AECD.
平面PEF,∴平面PEF⊥平面AECD.
∵在等腰梯形ABCD中,AD∥BC,AB=AD,∠ABC=60°,E是BC的中点,∴△ABE与△ADE都是等边三角形,∴BM⊥AE,DM⊥AE.∵BM∩DM=M,BM,DM
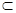 平面BDM,∴AE⊥平面BDM.∵BD
平面BDM,∴AE⊥平面BDM.∵BD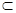 平面BDM,∴AE⊥BD.
平面BDM,∴AE⊥BD.(2)连结CM交EF于点N,连结PN.
∵ME∥FC,且ME=FC,∴四边形MECF是平行四边形,∴N是线段CM的中点.∵P是线段BC的中点,∴PN∥BM.∵BM⊥平面AECD,∴PN⊥平面AECD.∵PN
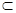 平面PEF,∴平面PEF⊥平面AECD.
平面PEF,∴平面PEF⊥平面AECD.
练习册系列答案
相关题目
 的底面
的底面 为一直角梯形,侧面PAD是等边三角形,其中
为一直角梯形,侧面PAD是等边三角形,其中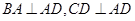 ,
, ,平面
,平面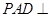 底面
底面 是
是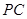 的中点.
的中点.
 //平面
//平面 ;
;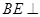
 ;
; 与平面
与平面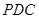 所成角的正弦值。
所成角的正弦值。 中,底面
中,底面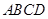 是矩形,
是矩形, 平面
平面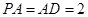 ,
, ,
,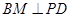 于点
于点 .
.

 ;
; 与平面
与平面 所成的角的余弦值.
所成的角的余弦值. ABCD是四棱锥,△ABD为正三角形,CB=CD,EC⊥BD.
ABCD是四棱锥,△ABD为正三角形,CB=CD,EC⊥BD.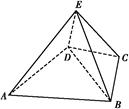

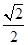 AD.若E、F分别为PC、BD的中点,求证:
AD.若E、F分别为PC、BD的中点,求证: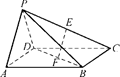
 ,
, ,
, ,则两直线PC与AB所成角的大小是______.
,则两直线PC与AB所成角的大小是______.