题目内容
如图,E是以AB为直径的半圆弧上异于A,B的点,矩形ABCD所在平面垂直于该半圆所在的平面,且AB=2AD=2。

(1).求证:EA⊥EC;
(2).设平面ECD与半圆弧的另一个交点为F。
①求证:EF//AB;
②若EF=1,求三棱锥E—ADF的体积

(1).求证:EA⊥EC;
(2).设平面ECD与半圆弧的另一个交点为F。
①求证:EF//AB;
②若EF=1,求三棱锥E—ADF的体积
(1)证明过程详见解析;(2)证明过程详见解析,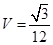 .
.
 .
.试题分析:本题主要考查线面的位置关系、几何体的体积等基础知识,意在考查考生的空间想象能力推理论证能力.第一问,由AB为圆的直径,得
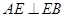 ,利用面面垂直的性质得
,利用面面垂直的性质得 平面
平面 ,再利用线面垂直的性质得到
,再利用线面垂直的性质得到 ,利用线面垂直的判定得
,利用线面垂直的判定得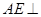 平面
平面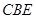 ,最后利用线面垂直即可得到所证结论;第二问,利用线面平行的判定得
,最后利用线面垂直即可得到所证结论;第二问,利用线面平行的判定得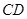 ∥平面
∥平面 ,利用线面平行的性质得
,利用线面平行的性质得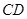 ∥
∥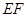 ,再根据平行线间的传递性得
,再根据平行线间的传递性得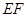 ∥
∥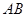 ,利用等体积转换法求三棱锥的体积.
,利用等体积转换法求三棱锥的体积.试题解析:(1)∵
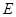 是半圆上异于
是半圆上异于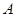 ,
,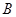 的点,∴
的点,∴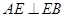 ,
,又∵平面
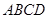
 平面
平面 ,且
,且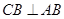 ,
,由面面垂直性质定理得
 平面
平面 ,
,又
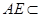 平面
平面 ,
,∴

∵
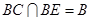 ,
,∴
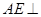 平面
平面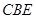
又
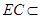 平面
平面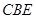
∴
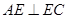 4分
4分(2)①由
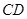 ∥
∥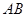 ,得
,得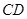 ∥平面
∥平面 ,
,又∵平面
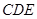
 平面
平面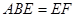 ,
,∴根据线面平行的性质定理得
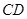 ∥
∥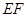 ,又
,又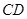 ∥
∥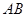 ,
,∴
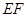 ∥
∥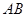 8分
8分②
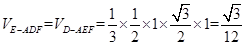 12分
12分
练习册系列答案
相关题目

 的底面
的底面 为一直角梯形,侧面PAD是等边三角形,其中
为一直角梯形,侧面PAD是等边三角形,其中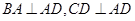 ,
, ,平面
,平面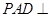 底面
底面 是
是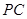 的中点.
的中点.
 //平面
//平面 ;
;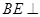
 ;
; 与平面
与平面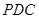 所成角的正弦值。
所成角的正弦值。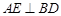 于
于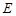 (不同于点
(不同于点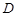 ),延长AE交BC于F,将△ABD沿BD折起,得到三棱锥
),延长AE交BC于F,将△ABD沿BD折起,得到三棱锥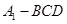 ,如图2所示.
,如图2所示.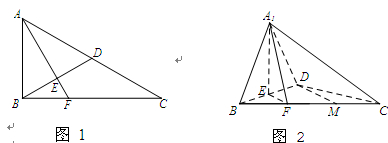
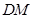 //平面
//平面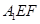 ;
;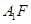 ;
;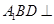 平面
平面 ,试判断直线
,试判断直线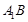 与直线CD能否垂直?并说明理由.
与直线CD能否垂直?并说明理由.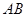 是圆
是圆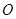 的直径,点
的直径,点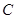 是圆
是圆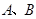 的点,直线
的点,直线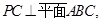
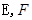 分别为
分别为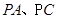 的中点。
的中点。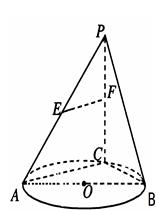
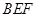 与平面
与平面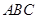 的交线为
的交线为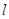 ,试判断
,试判断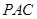 的位置关系,并加以说明;
的位置关系,并加以说明; ,且点
,且点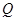 满足
满足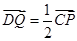 ,记直线
,记直线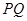
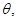 异面直线
异面直线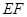 所成的锐角为
所成的锐角为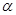 ,二面角
,二面角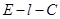 的大小为
的大小为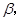
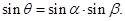
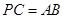 ,求直线
,求直线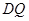 与平面
与平面
 是两个不同的平面,
是两个不同的平面, 是一条直线,以下命题:
是一条直线,以下命题: ,则
,则 ;②若
;②若 ,
, ,
,

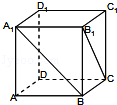
 的侧棱
的侧棱 在下底面的射影
在下底面的射影 与
与 平行,若
平行,若 ,且
,且 ,则
,则 的余弦值为( )
的余弦值为( )



