题目内容
【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() 所对的边分别为
所对的边分别为![]() ,
,![]() ,
,![]() ,过
,过![]() 作直线
作直线![]() 与边
与边![]() 相交于点
相交于点![]() ,
,![]() ,
,![]() .当直线
.当直线![]() 时,
时,![]() 值为
值为![]() ;当
;当![]() 为边
为边![]() 的中点时,
的中点时,![]() 值为
值为![]() .当
.当![]() ,
,![]() 变化时,记
变化时,记![]() (即
(即![]() 、
、![]() 中较大的数),则
中较大的数),则![]() 的最小值为( )
的最小值为( )
A.![]() B.
B.![]() C.
C.![]() D.1
D.1
【答案】C
【解析】
当直线![]() 时,由直角三角形的勾股定理和等面积法,可得出
时,由直角三角形的勾股定理和等面积法,可得出![]() ,
, ![]() ,再由基本不等式可得出
,再由基本不等式可得出![]() ,从而得出M的范围.当
,从而得出M的范围.当![]() 为边
为边![]() 的中点时,由直角三角形的斜边上的中线为斜边的一半和勾股定理可得
的中点时,由直角三角形的斜边上的中线为斜边的一半和勾股定理可得![]() ,
,![]() ,由基本不等式可得出
,由基本不等式可得出![]() ,从而得出
,从而得出![]() 的范围,可得选项.
的范围,可得选项.
当直线![]() 时,因为
时,因为![]() ,
,![]() ,所以
,所以![]() ,由等面积法得
,由等面积法得![]() ,
,
因为有![]() (当且仅当
(当且仅当![]() 时,取等号),即
时,取等号),即![]() ,所以
,所以![]() ,
,
所以![]() (当且仅当
(当且仅当![]() 时,取等号),
时,取等号),
当![]() 为边
为边![]() 的中点时,因为
的中点时,因为![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,
,
因为有![]() (当且仅当
(当且仅当![]() 时,取等号),即
时,取等号),即![]() ,所以
,所以![]() ,
,
所以![]() (当且仅当
(当且仅当![]() 时,取等号),
时,取等号),
当![]() ,
,![]() 变化时,记
变化时,记![]() (即
(即![]() 、
、![]() 中较大的数),则
中较大的数),则![]() 的最小值为
的最小值为![]() (此时,
(此时,![]() );
);
故选:C.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
【题目】某地植被面积 ![]() (公顷)与当地气温下降的度数
(公顷)与当地气温下降的度数![]() (
(![]() )之间有如下的对应数据:
)之间有如下的对应数据:
| 20 | 40 | 50 | 60 | 80 |
| 3 | 4 | 4 | 4 | 5 |
(1)请用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)根据(1)中所求线性回归方程,如果植被面积为200公顷,那么下降的气温大约是多少![]() ?
?
参考公式:用最小二乘法求线性回归方程系数公式: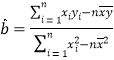 ,
,![]() .
.