题目内容
【题目】已知函数![]() ,其最小正周期为
,其最小正周期为![]() .
.
(1)求![]() 的表达式;
的表达式;
(2)将函数![]() 的图象向右平移
的图象向右平移![]() 个单位长度后,再将得到的图象上各点的横坐标伸长到原来的
个单位长度后,再将得到的图象上各点的横坐标伸长到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象,若关于
的图象,若关于![]() 的方程
的方程![]() 在区间
在区间![]() 上有且只有一个实数解,求实数
上有且只有一个实数解,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)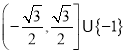 .
.
【解析】
(1)利用三角恒等变换思想化简函数![]() 的解析式为
的解析式为![]() ,利用函数
,利用函数![]() 的最小正周期可求得
的最小正周期可求得![]() 的值,由此可得出函数
的值,由此可得出函数![]() 的解析式;
的解析式;
(2)利用三角函数图象变换可得![]() ,由
,由![]() 可计算出
可计算出![]() 的取值范围,由
的取值范围,由![]() 可得
可得![]() ,可得出直线
,可得出直线![]() 与函数
与函数![]() 在区间
在区间![]() 上的图象有且只有一个交点,数形结合可求得实数
上的图象有且只有一个交点,数形结合可求得实数![]() 的取值范围.
的取值范围.
(1)![]()
![]() ,
,
又因为函数![]() 的最小正周期
的最小正周期![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
所以![]() ;
;
(2)将函数![]() 的图象向右平移
的图象向右平移![]() 个单位长度后,得到
个单位长度后,得到![]() 的图象.再将所得图象上所有点的横坐标伸长到原来的
的图象.再将所得图象上所有点的横坐标伸长到原来的![]() 倍(纵坐标不变),得到
倍(纵坐标不变),得到![]() 的图象,所以
的图象,所以![]() ,
,
当![]() 时,
时,![]() ,
,
令![]() ,可得
,可得![]() ,令
,令![]() ,可知直线
,可知直线![]() 与函数
与函数![]() 在区间
在区间![]() 上的图象有且只有一个交点,如下图所示:
上的图象有且只有一个交点,如下图所示:
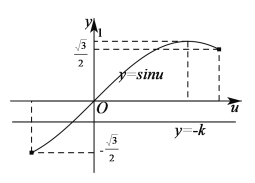
由图象可知,当![]() 或
或![]() 时,
时,
直线![]() 与函数
与函数![]() 在区间
在区间![]() 上的图象有且只有一个交点.
上的图象有且只有一个交点.
所以实数![]() 的取值范围是
的取值范围是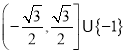 .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
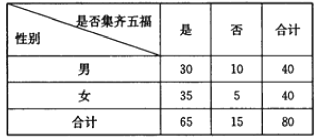
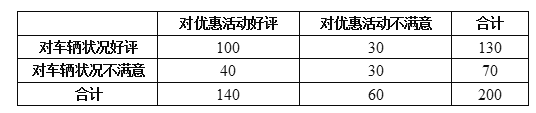
【题目】某企业三月中旬生产A、B、C三种产品共3 000件,根据分层抽样的结果,企业统计员制作了如下的统计表格:
产品类别 | A | B | C |
产品数量(件) | 1 300 | ||
样本容量(件) | 130 |
由于不小心,表格中A、C产品的有关数据已被污染看不清楚,统计员记得A产品的样本容量比C产品的样本容量多10,根据以上信息,可得C的产品数量是( )
A.80B.800C.90D.900