题目内容
【题目】如图所示,正三角形ABC所在平面与梯形BCDE所在平面垂直,![]() ,
,![]() =4 ,
=4 ,![]() ,F为棱AE的中点.
,F为棱AE的中点.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)若直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析,;(2)![]()
【解析】(1)如图,取![]() 中点
中点![]() ,连接
,连接![]() 、
、![]() ,因为
,因为![]() 为
为![]() 中点,所以
中点,所以![]() ,又
,又![]() ,
,![]() ,
,
所以![]() ,所以四边形
,所以四边形![]() 为平行四边形,所以
为平行四边形,所以![]() .又
.又![]() 为正三角形,所以
为正三角形,所以
![]() ,从而
,从而![]() , (2分)
, (2分)
由![]() ,
,![]() ,可得
,可得![]() ,由平面ABC
,由平面ABC![]() 平面BCDE,平面ABC
平面BCDE,平面ABC![]() 平面BCDE=BC,
平面BCDE=BC,
可得![]() 平面ABC,因为
平面ABC,因为![]() 平面ABC,所以
平面ABC,所以![]() ,
,
因为![]() ,所以
,所以![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .(5分)
.(5分)
(2)因为![]() ,
,![]() ,所以
,所以![]() ,又
,又![]() ,
,![]() ,
,
所以![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
所以![]() 为
为![]() 与平面
与平面![]() 所成的角,即
所成的角,即![]() ,从而
,从而![]() .(7分)
.(7分)
以![]() 为原点,建立如图所示的空间直角坐标系
为原点,建立如图所示的空间直角坐标系![]() ,
,
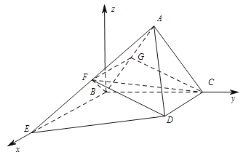
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,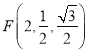 ,
,
所以![]() ,
,![]() .(8分)
.(8分)
设平面![]() 的法向量为
的法向量为![]() ,则
,则![]() ,即
,即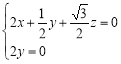 ,解得
,解得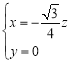 .
.
令![]() ,得
,得![]() .
.
由(1)可知![]() 平面
平面![]() ,所以
,所以![]() 为平面
为平面![]() 的一个法向量.
的一个法向量.
所以![]() .
.
因为二面角![]() 为钝角,所以其余弦值为
为钝角,所以其余弦值为![]() .(12分)
.(12分)

【题目】第十二届全国人民代表大会第五次会议和政协第十二届全国委员会第五次会议(简称两会)将分别于2017年3月5日和3月3日在北京开幕.全国两会召开前夕,某网站推出两会热点大型调查,调查数据表明,民生问题是百姓最为关心的热点,参与调查者中关注此问题的约占![]() .现从参与者中随机选出200人,并将这200人按年龄分组:第
.现从参与者中随机选出200人,并将这200人按年龄分组:第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,得到的频率分布直方图如图所示:
,得到的频率分布直方图如图所示:

(1)现在要从年龄较小的第1,2,3组中用分层抽样的方法抽取12人,再从这12人中随机抽取3人赠送礼品,求抽取的3人中至少有![]() 人年龄在第3组的概率;
人年龄在第3组的概率;
(2)若从所有参与调查的人(人数很多)中任意选出3人,记关注民生问题的人数为X,求X的分布列与期望;
(3)把年龄在第1,2,3组的居民称为青少年组,年龄在第4,5组的居民称为中老年组,若选出的200人中不关注民生问题的人中老年人有10人,问是否有![]() 的把握认为是否关注民生问题与年龄有关?
的把握认为是否关注民生问题与年龄有关?
附:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
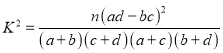 ,
,![]() .
.