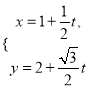Question

【题目】设函数 ． （I）求 的值；
（II）若f（a）＞f（﹣a），求实数a的取值范围．

Answer 1

【答案】解：（Ⅰ）f（﹣ ）=log0.5（ ）=2，f（2）=log22=1，∴ =1，
（Ⅱ）当x＞0时，f（x）=log2x，函数为增函数，
当x＜0时，f（x）=log0.5（﹣x），函数也为增函数，
∵f（a）＞f（﹣a），
当a＞0时，则log2a＞log0.5a=log2 ，即a＞ ，解得a＞1，
当a＜0时，则log0.5（﹣a）=log2（﹣a）即log2 ＞log2（﹣a），即﹣ ＞﹣a，解得﹣1＜a＜0
综上所述实数a的取值范围（﹣1，0）∪（1，+∞）
【解析】（Ⅰ）根据分段函数的解析，代值计算即可，（Ⅱ）对a进行分类讨论，即可求出a的取值范围．