题目内容
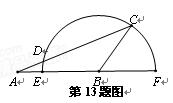
如图,在△ABC中,AC=3,AB=5,∠A=120°;
(1)求BC的长;
(2)求△ABC的边BC上的高AM的长.

(1)求BC的长;
(2)求△ABC的边BC上的高AM的长.

(1)在△ABC中,AC=3,AB=5,∠A=120°,
故由余弦定理得:BC2=AC2+AB2-2AC•ABcos∠BAC
=9+25-2×3×5×(-
)=49,
∴BC=7
(2)∵S△ABC=
AC•ABsin∠BAC
=
×3×5×
=
,
又S△ABC=
BC•AM=
×7AM,
∴
×7AM=
,
∴AM=
.
故由余弦定理得:BC2=AC2+AB2-2AC•ABcos∠BAC
=9+25-2×3×5×(-
| 1 |
| 2 |
∴BC=7
(2)∵S△ABC=
| 1 |
| 2 |
=
| 1 |
| 2 |
| ||
| 2 |
=
15
| ||
| 4 |
又S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
∴
| 1 |
| 2 |
15
| ||
| 4 |
∴AM=
15
| ||
| 14 |

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
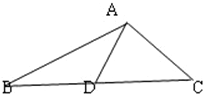
 中,
中,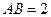 ,
,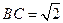 ,
,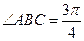 . 以点
. 以点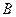 为圆心,线段
为圆心,线段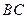 的长为半径的半圆分别交
的长为半径的半圆分别交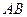 所在直线于点
所在直线于点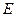 、
、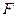 ,交线段
,交线段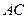 于点
于点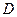 ,则弧
,则弧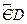 的长约为 .(精确到
的长约为 .(精确到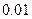 )
)