题目内容

如图，在△ABC中，AD是BC边上的中线，AB=5，AC=3，AD=2，求：BC的长及面积S△ABC．
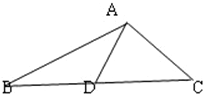
设BD=CD=x，
在△ABD和△ACD中，
cos∠ADB=
AD2+BD2-AB2
2AD•BD
，cos∠ADC=
AD2+DC2-AC2
2AD•DC
，
∵∠ADB+∠ADC=180°，
∴cos∠ADB+cos∠ADC=0，即4+x2-25+4+x2-9=0，
解得：x=
13
，
∴BC=2
13
，
在△ABC中，cosB=
AB2+BC2-AC2
2AB•BC
=
25+52-9
20
13
=
34
13
130
，
∴sinB=
1-cos2B
=
6
13
65
，
则S△ABC=
1
2
AB•BC•sinB=6．
练习册系列答案
相关题目
如图，在△ABC中，AC=3，AB=5，∠A=120°；
（1）求BC的长；
（2）求△ABC的边BC上的高AM的长．
在△ABC中，内角A，B，C的对边分别为a，b，c，若sinC=2sinA，b=
3
a．
（1）求角B；
（2）若△ABC的面积为2
3
，求函数f（x）=2sin2（x+π）+cos（2x-B）-a的单调增区间．
设△ABC的内角A，B，C所对的边分别为a，b，c，若c（1+cosA）=
3
a•sinC
（1）求角A的大小；
（2）若a=2，△ABC的面积为
3
，求△ABC的周长．
在△ABC中，已知C=120°，两边a和b是方程x2-3x+2=0的两根，则边c等于（　　）
A．
5
B．
7
C．
11
D．
13
在△ABC中，BC=
5
，AC=3，sinC=2sinA．
（1）求边长AB的值；
（2）求△ABC的面积．
设△ABC的内角A，B，C所对的边为a，b，c，则下列命题正确的是______（写出所有正确命题的序号）．
①若ab＞c2，则C＜
π
3
；
②若a+b＞2c，则C＜
π
3
；
③若a4+b4=c4，则C＜
π
2
；
④若（a+b）c＜2ab，则C＞
π
2
；
⑤若（a2+b2）c2＜2a2b2，则C＞
π
3
．
三角形的两边长分别为1，
3
，第三边上的中线长为1，则此三角形外接圆半径为______．
已知等差数列的前项和为，若，则 (     )
A．B．C．D．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网