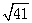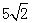题目内容

△ABC的三个内角A、B、C对应的三条边长分别是a、b、c，且满足csinA=
3
acosC．
（1）求角C的大小；
（2）若b=2，c=
7
，求a．
（1）由正弦定理
a
sinA
=
c
sinC
，得csinA=asinC，
由已知得csinA=asinC=
3
acosC，即tanC=
3
，
∵0＜C＜π，∴C=
π
3
；
（2）由余弦定理c2=a2+b2-2abcosC，得（
7
）2=a2+22-4acos
π
3
，即a2-2a-3=0，
解得：a=3或a=-1，负值舍去，
则a=3．
练习册系列答案
相关题目
在△ABC中，已知
a-c
b-c
=
b
a+c
，则角A为（　　）
A．30°B．60°C．120°D．150°
△ABC中，已知其面积为S=
1
4
(a2+b2-c2)，则角C的度数为（　　）
A．135°B．45°C．60°D．120°
如图，在△ABC中，AC=3，AB=5，∠A=120°；
（1）求BC的长；
（2）求△ABC的边BC上的高AM的长．
在△ABC中，角A，B，C的对边分别为a，b，c，若a=
3
，b+c=4，∠B=30°，则c=（　　）
A．
13
4
B．
12
5
C．3D．
13
5
在△ABC中，A最大，C最小，且A=2C，a+c=2b，求此三角形的三边之比．
设锐角三角形ABC的内角A，B，C的对边分别为a，b，c，b=
2
asinB．
（1）求A的大小；
（2）若b=
6
，c=
3
+1，求a．
在△ABC中，BC=
5
，AC=3，sinC=2sinA．
（1）求边长AB的值；
（2）求△ABC的面积．
A．5B．25C．D．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网