题目内容

在△ABC中，若三边a、b、c满足（a+b-c）（a+b+c）=ab．则角C=（　　）
A．
2π
3
B．
π
3
C．
π
6
D．
2π
3
或
π
3
∵（a+b-c）（a+b+c）=ab．
∴a2+b2-c2=-ab
由余弦定理cosC=
a2+b2-c2
2ab
=-
1
2

∵0＜C＜π
∴C=
2π
3
练习册系列答案
相关题目
△ABC中，B=60°，最大边与最小边之比为(
3
+1)：2，则最大角为（　　）
A．45°B．60°C．75°D．90°
如图，在△ABC中，AC=3，AB=5，∠A=120°；
（1）求BC的长；
（2）求△ABC的边BC上的高AM的长．
如图，海中小岛A周围40海里内有暗礁，一船正在向南航行，在B处测得小岛A在船的南偏东30°，航行30海里后，在C处测得小岛在船的南偏东45°，如果此船不改变航向，继续向南航行，问有无触礁的危险？
在△ABC中，A最大，C最小，且A=2C，a+c=2b，求此三角形的三边之比．
某观测站C在目标A的南偏西25°方向，从A出发有一条南偏东35°走向的公路，在C处测得与C相距31km的公路有一人正沿此公路向A走去，走20km到达D，此时测得CD=21km，求此人在D处距A还有多少千米．
在△ABC中，内角A，B，C的对边分别为a，b，c，若sinC=2sinA，b=
3
a．
（1）求角B；
（2）若△ABC的面积为2
3
，求函数f（x）=2sin2（x+π）+cos（2x-B）-a的单调增区间．
设△ABC的内角A，B，C所对的边为a，b，c，则下列命题正确的是______（写出所有正确命题的序号）．
①若ab＞c2，则C＜
π
3
；
②若a+b＞2c，则C＜
π
3
；
③若a4+b4=c4，则C＜
π
2
；
④若（a+b）c＜2ab，则C＞
π
2
；
⑤若（a2+b2）c2＜2a2b2，则C＞
π
3
．
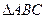锐角中已知两边a=1,b=2，则第三边c的取值范围是_________

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网