题目内容

若直线y=-x+m与曲线y=
5-
1
4
x2
只有一个公共点，则m的取值范围是（　　）
A．-1≤m＜2B．-2
5
≤m≤2
5
C．-2≤m＜2或m=5D．-2
5
≤m≤2
5
或m=5
根据曲线y=
5-
1
4
x2
，得到5-
1
4
x2≥0，解得：-2
5
≤x≤2
5
；y≥0，
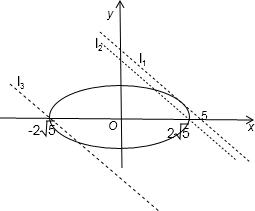
画出曲线的图象，为椭圆在x轴上边的一部分，如图所示：
当直线y=-x+m在直线l1的位置时，直线与椭圆相切，故只有一个交点，
把直线y=-x+m代入椭圆方程得：5x2-8mx+4m2-20=0，得到△=0，
即64m2-20（4m2-20）=0，化简得：m2=25，解得m=5或m=-5（舍去），
则m=5时，直线与曲线只有一个公共点；
当直线y=-x+m在直线l2位置时，直线与曲线刚好有两个交点，此时m=2
5
，
当直线y=-x+m在直线l3位置时，直线与曲线只有一个公共点，此时m=-2
5
，
则当-2
5
≤m＜2
5
时，直线与曲线只有一个公共点，
综上，满足题意得m的范围是-2
5
≤m＜2
5
或m=5．
故选D
练习册系列答案
相关题目
椭圆
x2
2
+y2=1的弦被点（
1
2
，
1
2
）平分，则这条弦所在的直线方程是______．
抛物线的顶点在原点O，焦点为椭圆
x2
3
+
y2
2
=1的右焦点F．
（1）求抛物线的方程；
（2）设点P在抛物线上运动，求P到直线y=x+3的距离的最小值，并求此时点P的坐标．
如图，从椭圆E：
x2
a2
+
y2
b2
=1(a＞b＞0)上一点P向x轴作垂线，垂足恰为左焦点F1，又点A是椭圆与x轴正半轴的交点，点B是椭圆与y轴正半轴的交点，且AB∥OP，|F1A|=
10
+
5
，
（1）求椭圆E的方程．
（2）是否存在圆心在原点的圆，使得该圆的任意一条切线与椭圆E恒有两个交点C，D，且
OC
⊥
OD
？若存在，写出该圆的方程，并求|CD|的取值范围；若不存在，说明理由．
已知椭圆E：
x2
a2
+
y2
b2
=1(a＞b＞0)的左、右焦点为F1，F2，且离心率为
3
2
．
（1）若过F1的直线交椭圆E于P，Q两点，且
PF1
=3
F1Q
，求直线PQ的斜率；
（2）若椭圆E过点（0，1），且过F1作两条互相垂直的直线，它们分别交椭圆E于A，C和B，D，求四边形ABCD面积的最大值和最小值．
已知椭圆E：
x2
a2
+y2=1（a＞1）的离心率e=
3
2
，直线x=2t（t＞0）与椭圆E交于不同的两点M、N，以线段MN为直径作圆C，圆心为C
（Ⅰ）求椭圆E的方程；
（Ⅱ）当圆C与y轴相切的时候，求t的值；
（Ⅲ）若O为坐标原点，求△OMN面积的最大值．
过双曲线
x2
3
-
y2
6
=1的右焦点F，倾斜角为30°的直线交此双曲线于A，B两点，求|AB|．
在平面直角坐标系xOy中，已知椭圆C1：
x2
a2
+
y2
b2
=1（a＞b＞0）的左焦点为F1（-1，0），且点P（0，1）在C1上．
（1）求椭圆C1的方程；
（2）设直线l同时与椭圆C1和抛物线C2：y2=4x相切，求直线l的方程．
椭圆的中心在原点，其左焦点F1与抛物线y2=-4x的焦点重合，过F1的直线l与椭圆交于A，B两点，与抛物线交于C，D两点．当直线l与x轴垂直时，
|CD|
|AB|
=2
2
．
（Ⅰ）求椭圆的方程；
（Ⅱ）求过点O，F1，并且与椭圆的左准线相切的圆的方程；
（Ⅲ）求
F2A
•
F2B
的最值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网