Question

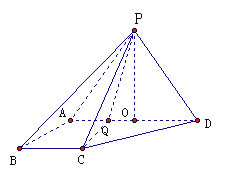
【题目】如图，在四棱锥P-ABCD中，侧面PAD⊥底面ABCD，侧棱，底面ABCD为直角梯形，其中，O为AD中点.

（1）求证：PO⊥平面ABCD；

（2）求直线BD与平面PAB所成角的正弦值；

（3）线段AD上是否存在点，使得它到平面PCD的距离为.

Answer 1

【答案】(1)见解析.

(2) .

（3）见解析.

【解析】

(1)先证明PO⊥AD,再证明PO⊥平面ABCD.(2)先证明∠DBP为直线BD与平面PAB所成角，再求直线BD与平面PAB所成角的正弦值.(3) 假设存在点Q，设QD＝x，再求出x的值.

（1）证明：在△PAD中PA=PD，O为AD中点，所以PO⊥AD,

又侧面PAD⊥底面ABCD，平面平面ABCD=AD, 平面PAD，

所以PO⊥平面ABCD.

（2）由（1）PO⊥平面ABCD，，又AB⊥AD，，

. ，，，，

为直线BD与平面PAB所成的角.

在Rt△DPB中，，，，

所以直线BD与平面PAB所成角的正弦值为.

（3）假设存在点Q，使得它到平面PCD的距离为.

设QD＝x，则，由（Ⅱ）得CD=OB=，

在Rt△POC中，

所以PC=CD=DP，

由VP-DQC=VQ-PCD 得，，

所以存在点Q满足题意，此时.