题目内容
【题目】函数f(x)=cos ![]() x,对任意的实数t,记f(x)在[t,t+1]上的最大值为M(t),最小值为m(t),则函数h(t)=M(t)﹣m(t)的值域为 .
x,对任意的实数t,记f(x)在[t,t+1]上的最大值为M(t),最小值为m(t),则函数h(t)=M(t)﹣m(t)的值域为 .
【答案】![]()
【解析】解:解:函数f(x)=cos ![]() x的周期为T=
x的周期为T= ![]() =4,1)当4n﹣1≤t≤4n,n∈Z,区间[t,t+1]为增区间,则有m(t)=cos
=4,1)当4n﹣1≤t≤4n,n∈Z,区间[t,t+1]为增区间,则有m(t)=cos ![]() ,M(t)=cos
,M(t)=cos ![]() =sin
=sin ![]() ,
,
2)当4n<t<4n+1,n∈Z,①若4n<t≤4n+ ![]() ,
,
则M(t)=1,m(t)=sin ![]() ,
,
②若4n+ ![]() <t<4n+1,则M(t)=1,m(t)=sin
<t<4n+1,则M(t)=1,m(t)=sin ![]() ,
,
3)当4n+1≤t≤4n+2,则区间[t,t+1]为减区间,则有M(t)=cos ![]() ,m(t)=sin
,m(t)=sin ![]() ;
;
4)当4n+2<t<4n+3,则m(t)=﹣1,
①当4n+2<t≤4n+ ![]() 时,M(t)=cos
时,M(t)=cos ![]() ,
,
②当4n+ ![]() <t<4n+3时,M(t)=sin
<t<4n+3时,M(t)=sin ![]() ;则有h(t)=M(t)﹣m(t)
;则有h(t)=M(t)﹣m(t)
= 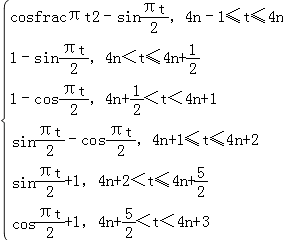
当4n﹣1≤t≤4n,h(t)的值域为[1, ![]() ],
],
当4n<t≤4n+ ![]() ,h(t)的值域为[1﹣
,h(t)的值域为[1﹣ ![]() ,1),
,1),
当4n+ ![]() <t<4n+1,h(t)的值域为(1﹣
<t<4n+1,h(t)的值域为(1﹣ ![]() ,1),
,1),
当4n+1≤t≤4n+2,h(t)的值域为[1, ![]() ],
],
当4n+2<t≤4n+ ![]() 时,h(t)的值域为[1﹣
时,h(t)的值域为[1﹣ ![]() ,1),
,1),
当4n+ ![]() <t<4n+3时,h(t)的值域为[1﹣
<t<4n+3时,h(t)的值域为[1﹣ ![]() ,1).
,1).
综上,h(t)=M(t)﹣m(t)的值域为 ![]() .
.
故答案是: ![]() .
.

 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案【题目】根据调查,某学校开设了“街舞”、“围棋”、“武术”三个社团,三个社团参加的人数如下表所示:
为调查社团开展情况,学校社团管理部采用分层抽样的方法从中抽取一个容量为n的样本,已知从“街舞”社团抽取的同学8人
社团 | 街舞 | 围棋 | 武术 |
人数 | 320 | 240 | 200 |
(Ⅰ)求n的值和从“围棋”社团抽取的同学的人数;
(Ⅱ)若从“围棋”社团抽取的同学中选出2人担任该社团活动监督的职务,已知“围棋”社团被抽取的同学中有2名女生,求至少有1名女同学被选为监督职务的概率.