题目内容
【题目】已知圆锥曲线![]() 的两个焦点坐标是
的两个焦点坐标是![]() ,且离心率为
,且离心率为![]() ;
;
(1)求曲线![]() 的方程;
的方程;
(2)设曲线![]() 表示曲线
表示曲线![]() 的
的![]() 轴左边部分,若直线
轴左边部分,若直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,求
两点,求![]() 的取值范围;
的取值范围;
(3)在条件(2)下,如果![]() ,且曲线
,且曲线![]() 上存在点
上存在点![]() ,使
,使![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)根据离心率可得曲线为双曲线,然后根据焦点及离心率可得![]() ,进而得到曲线方程.(2)将直线方程代入双曲线方程得到二次方程
,进而得到曲线方程.(2)将直线方程代入双曲线方程得到二次方程![]() ,根据题意可得该二次方程有两个负数根,结合根与系数的关系可得所求.(3)由弦长公式及(2)中实数
,根据题意可得该二次方程有两个负数根,结合根与系数的关系可得所求.(3)由弦长公式及(2)中实数![]() 的取值范围可得
的取值范围可得![]() ,于是可得直线AB的方程.设C(x0,y0),由条件
,于是可得直线AB的方程.设C(x0,y0),由条件![]() 可得
可得![]() ,再根据点
,再根据点![]() 在双曲线上可求得
在双曲线上可求得![]() .
.
(1)由e=![]() 知,曲线E是以F1(﹣
知,曲线E是以F1(﹣![]() ,0),F2(
,0),F2(![]() ,0)为焦点的双曲线,
,0)为焦点的双曲线,
且c=![]() ,
,![]() ,
,
解得![]() ,
,
∴b2=2﹣1=1,
故双曲线E的方程是x2﹣y2=1.
(2)由![]() 消去
消去![]() 整理得
整理得![]()
设A(x1,y1),B(x2,y2),
由题意可得方程有两个负数根,
∴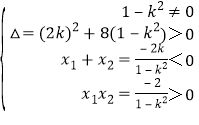 ,解得
,解得![]() ,
,
∴实数![]() 的取值范围是
的取值范围是![]() .
.
(3)由题意及(2)得
6![]() =|
=|![]() |=
|=![]() |x1﹣x2|=
|x1﹣x2|=![]()
![]() =
=![]() ,
,
整理得28k4﹣55k2+25=0,
解得![]() 或
或![]() ,
,
又﹣![]() ,
,
∴k=﹣![]() ,
,
故直线AB的方程为![]() .
.
设C(x0,y0),由![]() =m
=m![]() ,得(x1,y1)+(x2,y2)=(mx0,my0),
,得(x1,y1)+(x2,y2)=(mx0,my0),
又![]() =﹣4
=﹣4![]() ,y1+y2=k(x1+x2)﹣2=8,
,y1+y2=k(x1+x2)﹣2=8,
∴![]() .
.
∵点![]() 在曲线E上,
在曲线E上,
∴![]() ,解得m=±4,
,解得m=±4,
当m=﹣4时,所得的点在双曲线的右支上,不合题意,
∴m=4为所求.

 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案【题目】根据调查,某学校开设了“街舞”、“围棋”、“武术”三个社团,三个社团参加的人数如下表所示:
为调查社团开展情况,学校社团管理部采用分层抽样的方法从中抽取一个容量为n的样本,已知从“街舞”社团抽取的同学8人
社团 | 街舞 | 围棋 | 武术 |
人数 | 320 | 240 | 200 |
(Ⅰ)求n的值和从“围棋”社团抽取的同学的人数;
(Ⅱ)若从“围棋”社团抽取的同学中选出2人担任该社团活动监督的职务,已知“围棋”社团被抽取的同学中有2名女生,求至少有1名女同学被选为监督职务的概率.