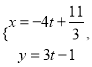题目内容
【题目】设圆上的点A(2,3)关于直线x+2y=0的对称点仍在圆上,且直线x-y+1=0被圆截得的弦长为2![]() ,求圆的方程.
,求圆的方程.
【答案】(x-6)2+(y+3)2=52或(x-14)2+(y+7)2=244.
【解析】试题分析:用待定系数法求解。设圆的方程为(x-a)2+(y-b)2=r2,根据圆心在直线![]() 上,点A(2,3)在圆上及弦长得到关于a,b,r的方程组,解方程组求得参数即可得到圆的方程。
上,点A(2,3)在圆上及弦长得到关于a,b,r的方程组,解方程组求得参数即可得到圆的方程。
试题解析:
设圆的方程为(x-a)2+(y-b)2=r2,
由题意,知直线x+2y=0过圆心,
∴a+2b=0.①
又点A在圆上,
∴(2-a)2+(3-b)2=r2.②
∵直线x-y+1=0被圆截得的弦长为![]() ,
,
∴ (![]() )2+
)2+![]() 2=r2.③
2=r2.③
由①②③可得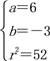 或
或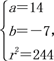
故所求圆的方程为(x-6)2+(y+3)2=52或(x-14)2+(y+7)2=244.

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案【题目】下表提供了某厂生产某产品过程中记录的产量![]() (吨)与相应的生产能耗
(吨)与相应的生产能耗![]() (吨标准煤)的几组对照数据:
(吨标准煤)的几组对照数据:
| 2 | 4 | 6 | 8 | 10 |
| 4 | 5 | 7 | 9 | 10 |
(1)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)根据(1)中求出的线性回归方程,预测生产20吨该产品的生产能耗是多少吨标准煤?
附:回归直线的斜率和截距的最小二乘估计分别为: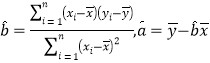 .
.
【题目】选修4—4:坐标系与参数方程.
已知曲线![]() 的参数方程为
的参数方程为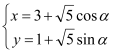 (
(![]() 为参数),以直角坐标系原点为极点,
为参数),以直角坐标系原点为极点,![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)若直线的极坐标方程为![]() ,求直线被曲线
,求直线被曲线![]() 截得的弦长.
截得的弦长.
【题目】2014年3月的“两会”上,李克强总理在政府工作报告中,首次提出“倡导全民阅读”,某学校响应政府倡导,在学生中发起读书热潮.现统计了从2014年下半年以来,学生每半年人均读书量,如下表:
时间 | 2014年下半年 | 2015年上半年 | 2015年下半年 | 2016年上半年 | 2016年下半年 |
时间代号 |
|
|
|
|
|
人均读书量 |
|
|
|
|
|
根据散点图,可以判断出人均读书量![]() 与时间代号
与时间代号![]() 具有线性相关关系.
具有线性相关关系.
(1)求![]() 关于
关于![]() 的回归方程
的回归方程![]() ;
;
(2)根据所求的回归方程,预测该校2017年上半年的人均读书量.
附:回归直线的斜率和截距的最小二乘估计公式分别为:
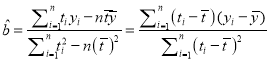 ,
, ![]()