题目内容
【题目】解答题。
(1)已知 ![]() 是奇函数,求常数m的值;
是奇函数,求常数m的值;
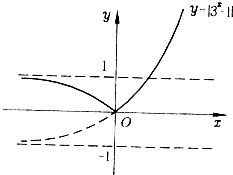
(2)画出函数y=|3x﹣1|的图象,并利用图象回答:k为何值时,方程|3x﹣1|=k无解?有一解?有两解?
【答案】
(1)解:因为3x﹣1≠0x≠0.故函数定义域为{x|x≠0}.
因为函数为奇函数,故有f(﹣1)=﹣f(1) ![]() m=1.
m=1.
所以所求常数m的值为1
(2)解:因为函数的零点即为对应两个函数图象的交点.所以把研究零点个数问题转化为研究图象交点个数.
当k<0时,直线y=k与函数y=|3x﹣1|的图象无交点,即方程无解;
当k=0或k≥1时,直线y=k与函数y=|3x﹣1|的图象有唯一的交点,所以方程有一解;
当0<k<1时,直线y=k与函数y=|3x﹣1|的图象有两个不同交点,所以方程有两解.
【解析】(1)先求出函数的定义域,再利用奇函数的定义,代入一对相反变量即可直接求常数m的值;(2)先取绝对值画出对应图象,再利用函数的零点即为对应两个函数图象的交点把y=k在图象上进行来回平移看交点个数即可找到结论.
【考点精析】根据题目的已知条件,利用函数奇偶性的性质的相关知识可以得到问题的答案,需要掌握在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇.

 天天练口算系列答案
天天练口算系列答案【题目】根据调查,某学校开设了“街舞”、“围棋”、“武术”三个社团,三个社团参加的人数如下表所示:
为调查社团开展情况,学校社团管理部采用分层抽样的方法从中抽取一个容量为n的样本,已知从“街舞”社团抽取的同学8人
社团 | 街舞 | 围棋 | 武术 |
人数 | 320 | 240 | 200 |
(Ⅰ)求n的值和从“围棋”社团抽取的同学的人数;
(Ⅱ)若从“围棋”社团抽取的同学中选出2人担任该社团活动监督的职务,已知“围棋”社团被抽取的同学中有2名女生,求至少有1名女同学被选为监督职务的概率.

