题目内容
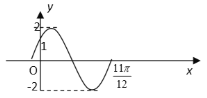
【题目】已知函数![]() ,且
,且![]() 的解集为
的解集为![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,对任意
,对任意![]() ,都有
,都有![]()
(1)求数列![]() 的通项公式.
的通项公式.
(2)已知数列![]() 的前
的前![]() 项和为
项和为![]() ,满足
,满足![]() ,
,![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() .
.
(3)已知数列![]() ,满足
,满足 ,若
,若 对任意
对任意![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]()
【解析】
(1)根据根与系数的关系求出![]() ,和
,和![]() ,再利用
,再利用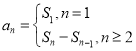 即可求出数列
即可求出数列![]() 的通项公式;
的通项公式;
(2)根据![]() ,
,![]() ,可证明
,可证明![]() 为等比数列,求得
为等比数列,求得![]() ,
,![]() ,再根据错位相减法即可求出结果;
,再根据错位相减法即可求出结果;
(3)由题意可知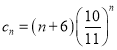 ,可得
,可得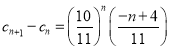 ,易知当
,易知当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,当
,当![]() 时,
时, ![]() ,进而求出有
,进而求出有![]() 的最大值为
的最大值为![]() ,再根据不等式恒成立可列出不等式,解不等式,即可求出结果.
,再根据不等式恒成立可列出不等式,解不等式,即可求出结果.
(1)![]() 的解集为
的解集为![]() ,∴
,∴![]() 是方程
是方程![]() 的两根
的两根
由韦达定理知![]() ,解得
,解得![]() ,∴
,∴![]() ,得
,得![]()
当![]() 时,有
时,有![]()
当![]() 时,有
时,有![]()
![]() 也符合
也符合![]() ,∴
,∴![]()
(2)当![]() 时,有
时,有![]() ,即
,即![]() ,得
,得![]()
当![]() 时,有
时,有![]() ,可得
,可得![]() ,即
,即![]() ,
,
∴![]() 为等比数列,首项为
为等比数列,首项为![]() ,公比为2,
,公比为2,
∴![]() ,∴
,∴![]() .
.
![]() ①,
①,
① ![]() 得,
得,![]() ②
②
①-②得![]()
∴![]()
(3)由题意可知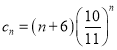 ,
,
则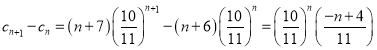
∴当![]() 时,
时,![]() ,即
,即![]()
当![]() 时,
时,![]() ,即
,即![]() ,
,
当![]() 时,
时,![]() ,即
,即![]() ,故有
,故有![]() 的最大值为
的最大值为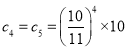
由于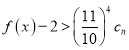 对任意
对任意![]() 恒成立
恒成立
则应有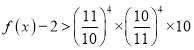 ,
,![]() 或
或![]()
综上:![]() 的取值范围是:
的取值范围是:![]() 或
或![]() .
.

练习册系列答案
 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目