��Ŀ����
20��ij���ƿ����μ������������ԣ���7�����У�4��������3���Ŀ��⣩���Żص�������ȡ3��������1����ÿ����ڵ�һ�γ鵽������������£��ڶ��κ͵����ξ��鵽�Ŀ���ĸ��ʣ�
��2���涨���ƿ��������������������һ���Ŀ��⣬�ÿ������������ĸ��ʾ�Ϊ$\frac{2}{3}$������Ŀ���ĸ��ʾ�Ϊ$\frac{1}{4}$����ÿ���Ե�10�֣��������֣��ָ����ѳ鵽�����⣨����һ�ģ������������ܷ�X�ķֲ�������ѧ����E��X����
���� ��1�������������ʹ�ʽ��������ÿ����ڵ�һ�γ鵽������������£��ڶ��κ͵����ξ��鵽�Ŀ���ĸ��ʣ�
��2��ȷ��X�Ŀ���ȡֵ�����ø��ʹ�ʽ���ɵõ��ܷ�X�ķֲ��У�����������ʽ���ɣ�
��� �⣺��1���ǡ��ÿ����ڵ�һ�γ鵽�����⡱Ϊ�¼�A�����ÿ����ڶ��κ͵����ξ��鵽�Ŀ��⡱Ϊ�¼�B����P��A��=$\frac{4}{7}$��P��AB��=$\frac{4}{35}$������2�֣�
��ÿ����ڵ�һ�γ鵽������������£��ڶ��κ͵����ξ��鵽�Ŀ���ĸ���ΪP��B|A��=$\frac{1}{5}$������5�֣�
��2��X�Ŀ���ȡֵΪ��0��10��20��30��
��P��X=0��=$\frac{1}{3}��\frac{1}{3}��\frac{3}{4}$=$\frac{1}{12}$��P��X=10��=${C}_{2}^{1}��\frac{2}{3}��\frac{1}{3}��\frac{3}{4}$+$��\frac{1}{3}��^{2}��\frac{1}{4}$=$\frac{13}{36}$��
P��X=20��=${C}_{2}^{2}����\frac{2}{3}��^{2}��\frac{3}{4}+{C}_{2}^{1}��\frac{1}{3}��\frac{2}{3}��\frac{1}{4}$=$\frac{4}{9}$��
P��X=30��=1-$\frac{1}{12}$-$\frac{13}{36}$-$\frac{4}{9}$=$\frac{1}{9}$������9�֣�
��X�ķֲ���Ϊ
| X | 0 | 10 | 20 | 30 |
| p | $\frac{1}{12}$ | $\frac{13}{36}$ | $\frac{4}{9}$ | $\frac{1}{9}$ |
��X����ѧ����ΪEX=0��$\frac{1}{12}$+10��$\frac{13}{36}$+20��$\frac{4}{9}$+30��$\frac{1}{9}$=$\frac{95}{6}$������12�֣�
���� ���⿼���˶����¼����������ʵĸ��ʹ�ʽ����������ķֲ��м����������ص㿼����ѧ�������������ȷ���⼰ȷ�ļ���������

| A�� | arcsin1=$\frac{��}{2}$ | B�� | arccos��-1��=�� | C�� | arctan0=0 | D�� | arccos1=2�� |
| A�� | $\frac{1}{2}$ | B�� | 1 | C�� | ������ | D�� | 0 |
| A�� | $\frac{{a}^{3}}{4}$ | B�� | $\frac{{a}^{3}}{3}$ | C�� | $\frac{{a}^{3}}{2}$ | D�� | $\frac{3{a}^{3}}{4}$ |
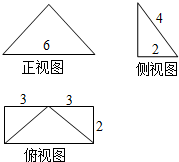
| A�� | 48 | B�� | 24$\sqrt{3}$ | C�� | 16 | D�� | 8$\sqrt{3}$ |
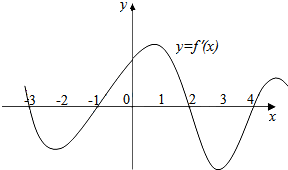 ��ͼ��y=f��x���ĵ�������ͼ����������˵����
��ͼ��y=f��x���ĵ�������ͼ����������˵����