题目内容
10.椭圆的中心在原点O,与双曲线2x2-2y2=1焦点相同,长轴长是2$\sqrt{2}$.(1)求椭圆方程;
(2)A是椭圆上一点,F1是椭圆左焦点,求$\overrightarrow{AO}•\overrightarrow{A{F_1}}$的范围.
分析 (1)通过双曲线的焦点为(-1,0)、(1,0),椭圆的长轴长2a=2$\sqrt{2}$,计算即得结论;
(2)通过设A(x1,y1),利用F1(-1,0)及点A满足椭圆方程化简$\overrightarrow{AO}•\overrightarrow{A{F_1}}$=$\frac{1}{2}$$({x}_{1}+1)^{2}$$+\frac{1}{2}$,进而通过x1∈[$-\sqrt{2}$,$\sqrt{2}$]即得结论.
解答 解:(1)∵双曲线2x2-2y2=1即$\frac{{x}^{2}}{\frac{1}{2}}-\frac{{y}^{2}}{\frac{1}{2}}=1$的焦点为(-1,0)、(1,0),
∴所求椭圆的焦点为(-1,0)、(1,0),
设椭圆方程为:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$,
则2a=2$\sqrt{2}$,即a=$\sqrt{2}$,
又∵a2-b2=1,∴b2=1,
∴椭圆方程为:$\frac{{x}^{2}}{2}+{y}^{2}=1$;
(2)设A(x1,y1),由(1)知F1(-1,0),
∴$\overrightarrow{AO}•\overrightarrow{A{F_1}}$=(-x1,-y1)•(-1-x1,-y1)
=${{x}_{1}}^{2}$+x1+${{y}_{1}}^{2}$
=${{x}_{1}}^{2}$+x1+(1-$\frac{1}{2}$${{x}_{1}}^{2}$)
=$\frac{1}{2}$${{x}_{1}}^{2}$+x1+1
=$\frac{1}{2}$$({x}_{1}+1)^{2}$$+\frac{1}{2}$,
∵x1∈[$-\sqrt{2}$,$\sqrt{2}$],
∴$\overrightarrow{AO}•\overrightarrow{A{F_1}}$∈[$\frac{1}{2}$,$\sqrt{2}+2$].
点评 本题是一道直线与圆锥曲线的综合题,考查运算求解能力,注意解题方法的积累,属于中档题.

 科学实验活动册系列答案
科学实验活动册系列答案| A. | 1 | B. | -1 | C. | i | D. | 0 |
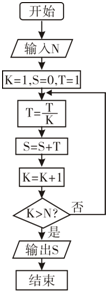
| A. | 1+$\frac{1}{2}+\frac{1}{3}+\frac{1}{4}$ | B. | 1+$\frac{1}{2}$+$\frac{1}{3×2}$+$\frac{1}{4×3×2}$ | ||
| C. | 1+$\frac{1}{2}+\frac{1}{3}+\frac{1}{4}$+$\frac{1}{5}$ | D. | 1+$\frac{1}{2}$+$\frac{1}{3×2}$+$\frac{1}{4×3×2}$+ |
(1)“?x∈R,2x+5>0”是全称命题;
(2)命题“?x∈R,x2+5x=6”的否定是“?x0∉R,使x02+5x0≠6”;
(3)若|x|=|y|,则x=y;
(4)若p∨q为假命题,则p、q均为假命题.
其中真命题的序号是( )
| A. | (1)(2) | B. | (2)(4) | C. | (1)(4) | D. | (1)(2)(3)(4) |
| A. | 若求得的回归方程为$\widehat{y}$=0.9x-0.3,则变量y和x之间具有正的相关关系 | |
| B. | 样本数据得到的回归直线必过样本点的中心($\overline{x}$,$\overline{y}$) | |
| C. | 残差平方和$\sum_{i=1}^{n}$(yi-$\widehat{y}$i)2越小,说明拟合的效果越好 | |
| D. | 用相关指数R2=1-$\frac{\sum_{i=1}^{n}({y}_{i}-\widehat{{y}_{i}})^{2}}{\sum_{i=1}^{n}({y}_{i}-\overline{y})^{2}}$刻画回归效果,R2的值越小,说明拟合的效果越好 |