题目内容
11.已知函数f(x)=$\frac{1}{{2}^{x}+1}$,写出求f(-4)+f(-3)+f(-2)+…+f(4)的一个算法,并画出程序框图.分析 可用循环结构计算f(-4)+f(-3)+f(-2)+…+f(4)的值,为累加运算,可令循环变量的初值为-4,终值为4,步长为1,由此确定循环前和循环体中各语句,即可得到相应的算法,最后根据算法画出相应的流程图即可.
解答 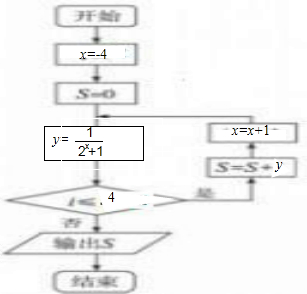 解:第一步:设x的值为-4;
解:第一步:设x的值为-4;
第二步:设s的值为0;
第三步:计算y=$\frac{1}{{2}^{x}+1}$,
第四步:如果i≤4执行第五步;否则转去执行第八步;
第五步:计算s+y并将结果代替s;
第六步:计算x+1并将结果代替x,
第七步:转去执行第三步;
第八步:输出s的值并结束算法.
点评 本题考查的知识点是设计程序框图解决实际问题,其中熟练掌握利用循环进行累加和累乘运算的方法,是解答本题的关键,属于中档题.

练习册系列答案
相关题目
17.已知集合P={x|y=lg(2-x)},Q={x|x2-5x+4≤0},则P∩Q=( )
| A. | {x|1≤x<2} | B. | {x|1<x<2} | C. | {x|0<x<4} | D. | {x|0≤x≤4} |
19.函数y=sinx+ex的图象上一点(0,1)处的切线的斜率为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 0 |
1.总体由编号为01,02,…,19,20的20个个体组成.利用下面的随机数表选取6个个体,选取方法是从随机数表第1行的第5列和第6列数字开始由左到右依次选取两个数字,则选出来的第6个个体的编号为( )
( )
| 7816 | 6572 | 0802 | 6314 | 0702 | 4369 | 9728 | 0198 |
| 3204 | 9234 | 4935 | 8200 | 3623 | 4869 | 6938 | 7481 |
| A. | 07 | B. | 04 | C. | 02 | D. | 01 |