题目内容
2．箱子里有3双不同的手套，随机拿出2只，记事件A表示“拿出的手套配不成对”；事件B表示“拿出的都是同一只手上的手套”；事件C表示“拿出的手套一只是左手的，一只是右手的，但配不成对”．（1）请罗列出所有的基本事件；
（2）分别求事件A、事件B、事件C的概率．
分析 （1）分别设3双手套为：a1a2；b1b2；c1c2．a1，b1，c1分别代表左手手套，a2，b2，c2分别代表右手手套．可列出所有的基本事件，
（2）分别求出事件A、事件B、事件C包含的基本事件个数，代入古典概型概率计算公式，可得答案．
解答 解：3双不同的手套标号为a1a2，b1b2，c1c2，a1，b1，c1分别代表左手手套，a2，b2，c2分别代表右手手套．
（1）所有基本事件总数为15种分别为：
a1a2，a1b1，a1b2，a1c1，a1c2，a2b1，a2b2，a2c1，a2c2，b1b2，b1c1，b1c2，b2c1，b2c2，c1c2…（5分）
（2）事件A包含的基本事件总数为12种，
分别为：a1b1，a1b2，a1c1，a1c2，a2b1，a2b2，a2c1，a2c2，b1c1，b1c2，b2c1，b2c2，
故$P（A）=\frac{4}{5}$；
事件B包含的基本事件总数为6种，
分别为：a1b1，a1c1，a2b2，a2c2，b1c1，b2c2，
故$P（B）=\frac{2}{5}$；
事件C包含的基本事件总数为6种，
分别为：a1b2，a1c2，a2b1，a2c1，b1c2，b2c1，
$P（C）=\frac{2}{5}$．…（10分）
点评 本题考查的知识点是古典概型概率计算公式，其中熟练掌握利用古典概型概率计算公式求概率的步骤，是解答的关键．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
8．
通过市场调查，得到某产品的资金投入x（万元）与获得的利润y（万元）的数据，如表所示：
（1）画出表中数据对应的散点图；
（2）根据上表提供的数据，用最小二乘法求线性回归直线方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$；
（3）现投入资金15（万元），估计获得的利润为多少万元？
参考公式：
用最小二乘法求线性回归方程系数公式：$\stackrel{∧}{b}$=$\frac{\sum_{i-1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i-1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$，$\stackrel{∧}{a}$=$\overline{y}$=$\stackrel{∧}{b}$$\overline{x}$．
通过市场调查，得到某产品的资金投入x（万元）与获得的利润y（万元）的数据，如表所示：| 资金投入 x | 2 | 3 | 4 | 5 | 6 |
| 利润y | 2 | 3 | 5 | 7 | 8 |
（2）根据上表提供的数据，用最小二乘法求线性回归直线方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$；
（3）现投入资金15（万元），估计获得的利润为多少万元？
参考公式：
用最小二乘法求线性回归方程系数公式：$\stackrel{∧}{b}$=$\frac{\sum_{i-1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i-1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$，$\stackrel{∧}{a}$=$\overline{y}$=$\stackrel{∧}{b}$$\overline{x}$．
10．已知a∈R，若关于x的方程x2+x-|a+$\frac{1}{4}$|+a2=0没有实根，则a的取值范围是（ ）
| A． | （-∞，-1）∪（$\frac{1+\sqrt{3}}{2}$，+∞） | B． | （-∞，$\frac{-1+\sqrt{3}}{2}$）∪（1，+∞） | ||
| C． | （-∞，-1）∪（1，+∞） | D． | （-∞，$\frac{-1-\sqrt{3}}{2}$）∪（$\frac{1+\sqrt{3}}{2}$，+∞） |
17．
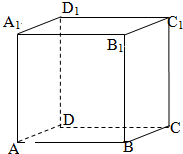ABCD-A1B1C1D1是单位正方体，黑白两只蚂蚁从点A出发沿棱向前爬行，每爬完一条棱称为“爬完一段”．白蚂蚁爬行的路线是AA1→A1D1，…，黑蚂蚁爬行的路线是AB→BB1，…，它们都遵循如下规则：所爬行的第i+2段与第i段所在直线必须是异面直线（i∈N*），设黑白蚂蚁都爬完2015段后各自停止在正方体的某个顶点处，则此时黑白蚂蚁的距离是（ ）
ABCD-A1B1C1D1是单位正方体，黑白两只蚂蚁从点A出发沿棱向前爬行，每爬完一条棱称为“爬完一段”．白蚂蚁爬行的路线是AA1→A1D1，…，黑蚂蚁爬行的路线是AB→BB1，…，它们都遵循如下规则：所爬行的第i+2段与第i段所在直线必须是异面直线（i∈N*），设黑白蚂蚁都爬完2015段后各自停止在正方体的某个顶点处，则此时黑白蚂蚁的距离是（ ）| A． | $\sqrt{2}$ | B． | 1 | C． | 0 | D． | $\sqrt{3}$ |
12．已知非零向量$\overrightarrow{a}$，$\overline{b}$满足（$\overrightarrow{a}$+$\overrightarrow{b}$）⊥（$\overrightarrow{a}$-$\overrightarrow{b}$），则（ ）
| A． | $\overrightarrow{a}$=$\overrightarrow{b}$ | B． | |$\overrightarrow{a}$|=|$\overrightarrow{b}$| | C． | $\overrightarrow{a}$⊥$\overrightarrow{b}$ | D． | $\overrightarrow{a}$∥$\overrightarrow{b}$ |