题目内容
20.某工厂生产已知产品的总利润L(元)与产量x(件)的函数关系式为L=-x2+bx+c(0<x<200),且生产10件产品时总利润为1800元,生产20件产品时总利润为3500元.(1)求L的解析式;
(2)产量是多少时,总利润最大?最大利润是多少?
分析 (1)利用生产10件产品时总利润为1800元,生产20件产品时总利润为3500元,建立方程,求出b,c,即可求L的解析式;
(2)配方,由此得出,当x=100时,函数L达到最大值9900元.
解答 解:(1)∵生产10件产品时总利润为1800元,生产20件产品时总利润为3500元,
∴$\left\{\begin{array}{l}{-100+10b+c=1800}\\{-400+20b+c=3500}\end{array}\right.$,
∴b=200,c=-100,
∴L=-x2+200x-100(0<x<200);
(2)将此函数表达式配方得,L=-(x-100)2+9900.
由此得出,当x=100时,函数L达到最大值9900元.
点评 本题主要考查利用数学知识解决实际问题,考查求二次函数在闭区间上的最值,求函数的最值,二次函数的性质的应用,属于中档题.

练习册系列答案
 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
10.已知a∈R,若关于x的方程x2+x-|a+$\frac{1}{4}$|+a2=0没有实根,则a的取值范围是( )
| A. | (-∞,-1)∪($\frac{1+\sqrt{3}}{2}$,+∞) | B. | (-∞,$\frac{-1+\sqrt{3}}{2}$)∪(1,+∞) | ||
| C. | (-∞,-1)∪(1,+∞) | D. | (-∞,$\frac{-1-\sqrt{3}}{2}$)∪($\frac{1+\sqrt{3}}{2}$,+∞) |
8.在数列{an}中,an=2(n-2)×3n-1,则数列{an}的前n项和Tn等于( )
| A. | $\frac{(2n-1){3}^{n}+5}{2}$ | B. | $\frac{(2n-3){3}^{n}+5}{2}$ | C. | $\frac{(2n-5){3}^{n}+5}{2}$ | D. | $\frac{(2n+5){3}^{n}+5}{2}$ |
15.学生“如花姐”是2015年我校高一年级“校园歌手大赛”的热门参赛选手之一,经统计,网络投票环节中大众对“如花姐”的投票情况是:
现采用分抽样的方法从所有参与“如花姐”投票的800名观众中抽取一个样本容量为n的样本,若从不喜欢“如花姐”的100名观众中抽取的人数是5人.
(1)求n的值;
(2)若不喜欢“如花姐”的1观众中抽取的5人中恰好3名男生(记为a1,a2,a3)2名女生(记为b1,b2),现将5人看成一个总体,从中随机选出2人,列出所有可能的结果;
(3)在(2)的条件下,求选出的2人中至少有1名女生的概率.
| 喜爱程度 | 非常喜欢 | 一般 | 不喜欢 |
| 人数 | 500 | 200 | 100 |
(1)求n的值;
(2)若不喜欢“如花姐”的1观众中抽取的5人中恰好3名男生(记为a1,a2,a3)2名女生(记为b1,b2),现将5人看成一个总体,从中随机选出2人,列出所有可能的结果;
(3)在(2)的条件下,求选出的2人中至少有1名女生的概率.
5.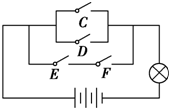 一个电路如图所示,C、D、E、F为4个开关,其闭合的概率都是$\frac{1}{2}$,且是相互独立的,则灯亮的概率是( )
一个电路如图所示,C、D、E、F为4个开关,其闭合的概率都是$\frac{1}{2}$,且是相互独立的,则灯亮的概率是( )
 一个电路如图所示,C、D、E、F为4个开关,其闭合的概率都是$\frac{1}{2}$,且是相互独立的,则灯亮的概率是( )
一个电路如图所示,C、D、E、F为4个开关,其闭合的概率都是$\frac{1}{2}$,且是相互独立的,则灯亮的概率是( )| A. | $\frac{9}{16}$ | B. | $\frac{7}{16}$ | C. | $\frac{13}{16}$ | D. | $\frac{3}{16}$ |
12.已知非零向量$\overrightarrow{a}$,$\overline{b}$满足($\overrightarrow{a}$+$\overrightarrow{b}$)⊥($\overrightarrow{a}$-$\overrightarrow{b}$),则( )
| A. | $\overrightarrow{a}$=$\overrightarrow{b}$ | B. | |$\overrightarrow{a}$|=|$\overrightarrow{b}$| | C. | $\overrightarrow{a}$⊥$\overrightarrow{b}$ | D. | $\overrightarrow{a}$∥$\overrightarrow{b}$ |
9.如图程序框图运行之后输出的W值为( )
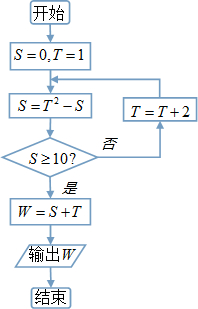

| A. | 11 | B. | 22 | C. | 39 | D. | 41 |