题目内容
19.函数y=sinx+ex的图象上一点(0,1)处的切线的斜率为( )| A. | 1 | B. | 2 | C. | 3 | D. | 0 |
分析 求出原函数的导函数,得到函数y=ex在x=1处的导数,即函数y=ex在x=1处的切线的斜率.
解答 解:由y=sinx+ex,得y′=cosx+ex,
∴y′|x=0=cos0+e0=2.
即函数y=sinx+ex的图象上一点(0,1)处的切线的斜率为2.
故选:B.
点评 本题考查利用导数研究曲线上某点处的切线方程,过曲线上某点处的切线的斜率,就是函数在该点处的导数值,是中档题.

练习册系列答案
相关题目
10.已知a∈R,若关于x的方程x2+x-|a+$\frac{1}{4}$|+a2=0没有实根,则a的取值范围是( )
| A. | (-∞,-1)∪($\frac{1+\sqrt{3}}{2}$,+∞) | B. | (-∞,$\frac{-1+\sqrt{3}}{2}$)∪(1,+∞) | ||
| C. | (-∞,-1)∪(1,+∞) | D. | (-∞,$\frac{-1-\sqrt{3}}{2}$)∪($\frac{1+\sqrt{3}}{2}$,+∞) |
8.在数列{an}中,an=2(n-2)×3n-1,则数列{an}的前n项和Tn等于( )
| A. | $\frac{(2n-1){3}^{n}+5}{2}$ | B. | $\frac{(2n-3){3}^{n}+5}{2}$ | C. | $\frac{(2n-5){3}^{n}+5}{2}$ | D. | $\frac{(2n+5){3}^{n}+5}{2}$ |
9.如图程序框图运行之后输出的W值为( )
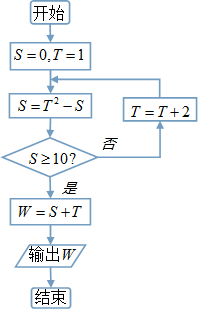

| A. | 11 | B. | 22 | C. | 39 | D. | 41 |