题目内容
16．计算：sin220+cos220+$\sqrt{3}$sin20°•cos80°．分析 见到平方式就降幂，见到乘积式就积化和差，将后两项积化和差，结合特殊角的三角函数值即可解决．
解答 解：原式=sin220+cos220+$\sqrt{3}$sin20°•cos（60°+20°）
=1+$\frac{\sqrt{3}}{2}$sin20°cos20°-$\frac{3}{2}$sin220°
=1+$\frac{\sqrt{3}}{4}$sin40°-$\frac{3}{4}$+$\frac{3}{4}$cos40°
=$\frac{1}{4}$+$\frac{\sqrt{3}}{2}$sin100°=$\frac{1}{4}$+$\frac{\sqrt{3}}{2}$cos10°
点评 本题主要考查了两角和与差、二倍角的三角函数的特殊值，属于基础题．
练习册系列答案
名校提分一卷通系列答案
课程达标测试卷闯关100分系列答案
新卷王期末冲刺100分系列答案
全能闯关100分系列答案
相关题目
8．在数列{an}中，an=2（n-2）×3n-1，则数列{an}的前n项和Tn等于（ ）
| A． | $\frac{（2n-1）{3}^{n}+5}{2}$ | B． | $\frac{（2n-3）{3}^{n}+5}{2}$ | C． | $\frac{（2n-5）{3}^{n}+5}{2}$ | D． | $\frac{（2n+5）{3}^{n}+5}{2}$ |
5．
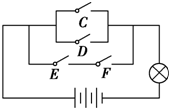一个电路如图所示，C、D、E、F为4个开关，其闭合的概率都是$\frac{1}{2}$，且是相互独立的，则灯亮的概率是（ ）
一个电路如图所示，C、D、E、F为4个开关，其闭合的概率都是$\frac{1}{2}$，且是相互独立的，则灯亮的概率是（ ）| A． | $\frac{9}{16}$ | B． | $\frac{7}{16}$ | C． | $\frac{13}{16}$ | D． | $\frac{3}{16}$ |