题目内容
1.在△ABC中,角A,B,C的对边分别为a,b,c,满足$\frac{a}{sinA}$=$\frac{b}{\sqrt{3}cosB}$(1)求∠B.
(2)若点M为BC中点,且AM=AC,求sin∠BAC的值.
分析 (1)由正弦定理、商的关系化简$\frac{a}{sinA}=\frac{b}{\sqrt{3}cosB}$,求出tanB的值,由内角的范围求出角B的值;
(2)设AB=c、BC=a,在△ABC、△ABM中由余弦定理求出AC、AM,由条件建立方程化简后得到a与c的关系式,代入式子求出AC,在△ABC中由正弦定理求出sin∠BAC的值.
解答 解:(1)由题意得,$\frac{a}{sinA}=\frac{b}{\sqrt{3}cosB}$,
则根据正弦定理得,$\frac{sinA}{sinA}=\frac{sinB}{\sqrt{3}cosB}$,所以tanB=$\sqrt{3}$,
又0<B<π,则B=$\frac{π}{3}$;
(2)设AB=c、BC=a,
在△ABC中,由余弦定理得AC2=a2+c2-2accosB=a2+c2-ac,
在△ABM中同理可得${AM}^{2}=(\frac{a}{2})^{2}+{c}^{2}-2•\frac{a}{2}ccosB$=$\frac{{a}^{2}}{4}+{c}^{2}-\frac{1}{2}ac$,
因为AM=AC,所以a2+c2-ac=$\frac{{a}^{2}}{4}+{c}^{2}-\frac{1}{2}ac$,
化简得3a=2c,代入AC2=a2+c2-2accosB得,
${AC}^{2}={a}^{2}+{(\frac{3a}{2})}^{2}-a•\frac{3a}{2}$=$\frac{7}{4}{a}^{2}$,则AC=$\frac{\sqrt{7}}{2}a$,
在△ABC中,由正弦定理得$\frac{AC}{sinB}=\frac{BC}{sin∠BAC}$,
则sin∠BAC=$\frac{BCsinB}{AC}$=$\frac{a×\frac{\sqrt{3}}{2}}{\frac{\sqrt{7}}{2}a}$=$\frac{\sqrt{21}}{7}$.
点评 本题考查正弦、余弦定理应用,考查化简、变形能力,注意内角的范围,属于中档题.

 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既非充分也非必要条件 |
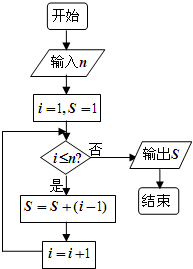
| A. | 7 | B. | 6 | C. | 5 | D. | 4 |
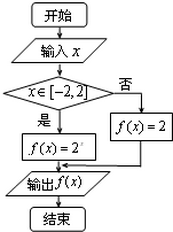 阅读程序框图,如果输出的函数值在区间[2,4]内,则输入的实数x的取值范围是( )
阅读程序框图,如果输出的函数值在区间[2,4]内,则输入的实数x的取值范围是( )| A. | (-∞,-2] | B. | (-∞,-2) | C. | [1,+∞) | D. | (-∞,-2)∪[1,+∞) |
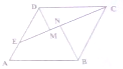 如图,菱形ABCD中,AB=1,∠ABC=$\frac{2}{3}$π,E为线段AD的动点,设∠ECD=α.
如图,菱形ABCD中,AB=1,∠ABC=$\frac{2}{3}$π,E为线段AD的动点,设∠ECD=α.