题目内容
在平面直角坐标系上,设不等式组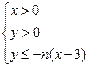 (
(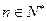 )
)
所表示的平面区域为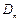 ,记
,记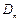 内的整点(即横坐标和纵坐标均为整数的点)的个数为
内的整点(即横坐标和纵坐标均为整数的点)的个数为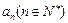 .
.
(Ⅰ)求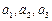 并猜想
并猜想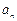 的表达式再用数学归纳法加以证明;
的表达式再用数学归纳法加以证明;
(Ⅱ)设数列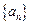 的前
的前 项和为
项和为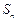 ,数列
,数列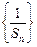 的前
的前 项和
项和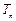 ,是否存在自然数m?使得对一切
,是否存在自然数m?使得对一切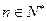 ,
,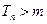 恒成立。若存在,求出m的值,若不存在,请说明理由。
恒成立。若存在,求出m的值,若不存在,请说明理由。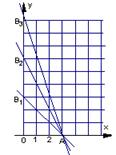
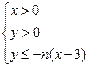 (
(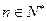 )
)所表示的平面区域为
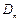 ,记
,记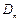 内的整点(即横坐标和纵坐标均为整数的点)的个数为
内的整点(即横坐标和纵坐标均为整数的点)的个数为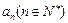 .
.(Ⅰ)求
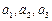 并猜想
并猜想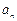 的表达式再用数学归纳法加以证明;
的表达式再用数学归纳法加以证明;(Ⅱ)设数列
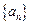 的前
的前 项和为
项和为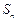 ,数列
,数列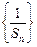 的前
的前 项和
项和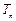 ,是否存在自然数m?使得对一切
,是否存在自然数m?使得对一切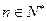 ,
,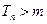 恒成立。若存在,求出m的值,若不存在,请说明理由。
恒成立。若存在,求出m的值,若不存在,请说明理由。
(Ⅰ)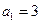 ,
,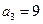 ,
,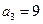 ,
,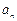 =3n,(Ⅱ)满足题设的自然数m存在,其值为0
=3n,(Ⅱ)满足题设的自然数m存在,其值为0
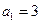 ,
,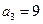 ,
,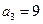 ,
,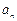 =3n,(Ⅱ)满足题设的自然数m存在,其值为0
=3n,(Ⅱ)满足题设的自然数m存在,其值为0(Ⅰ)当n=1时,D1为Rt△OAB1的内部包括斜边,这时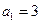
 ,
,
当n=2时,D2为Rt△OAB2的内部包括斜边,这时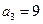
 ,
,
当n=3时,D3为Rt△OAB3的内部包括斜边,这时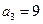
 ,……, ---3分
,……, ---3分
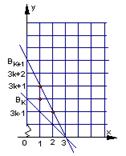 由此可猜想
由此可猜想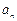 =3n。 --------------------------------------------------4分
=3n。 --------------------------------------------------4分
下面用数学归纳法证明:
(1)当n=1时,猜想显然成立。
(2)假设当n=k时,猜想成立,即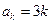 ,(
,(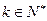 ) ----5分
) ----5分
如图,平面区域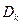 为Rt
为Rt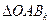 内部包括斜边、平面区域
内部包括斜边、平面区域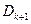 为
为
Rt△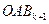 内部包括斜边,∵平面区域
内部包括斜边,∵平面区域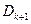 比平面区域
比平面区域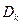 多3
多3
个整点, ------- 7分
即当n=k+1时,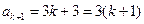 ,这就是说当n=k+1时,
,这就是说当n=k+1时,
猜想也成立,
由(1)、(2)知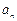 =3n对一切
=3n对一切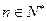 都成立。 ---------------------8分
都成立。 ---------------------8分
(Ⅱ)∵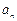 =3n, ∴数列
=3n, ∴数列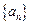 是首项为3,公差为3的等差数列,
是首项为3,公差为3的等差数列,
∴ .
.
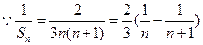 -------------------------10分
-------------------------10分
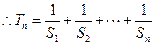
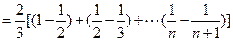
=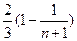 =
=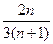 -------------------------------11分
-------------------------------11分
∵对一切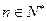 ,
,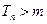 恒成立, ∴
恒成立, ∴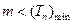
∵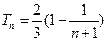 在
在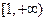 上为增函数 ∴
上为增函数 ∴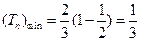 ---13分
---13分
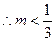 ,满足
,满足 的自然数为0,
的自然数为0,
∴满足题设的自然数m存在,其值为0。 -------------------------14分
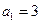
 ,
,当n=2时,D2为Rt△OAB2的内部包括斜边,这时
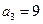
 ,
,当n=3时,D3为Rt△OAB3的内部包括斜边,这时
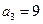
 ,……, ---3分
,……, ---3分 由此可猜想
由此可猜想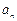 =3n。 --------------------------------------------------4分
=3n。 --------------------------------------------------4分下面用数学归纳法证明:
(1)当n=1时,猜想显然成立。
(2)假设当n=k时,猜想成立,即
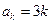 ,(
,(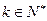 ) ----5分
) ----5分如图,平面区域
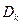 为Rt
为Rt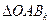 内部包括斜边、平面区域
内部包括斜边、平面区域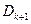 为
为Rt△
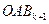 内部包括斜边,∵平面区域
内部包括斜边,∵平面区域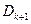 比平面区域
比平面区域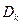 多3
多3个整点, ------- 7分
即当n=k+1时,
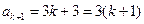 ,这就是说当n=k+1时,
,这就是说当n=k+1时,猜想也成立,
由(1)、(2)知
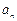 =3n对一切
=3n对一切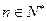 都成立。 ---------------------8分
都成立。 ---------------------8分(Ⅱ)∵
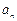 =3n, ∴数列
=3n, ∴数列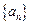 是首项为3,公差为3的等差数列,
是首项为3,公差为3的等差数列,∴
 .
. 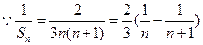 -------------------------10分
-------------------------10分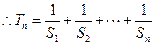
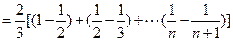
=
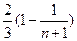 =
=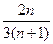 -------------------------------11分
-------------------------------11分∵对一切
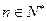 ,
,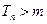 恒成立, ∴
恒成立, ∴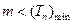
∵
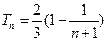 在
在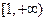 上为增函数 ∴
上为增函数 ∴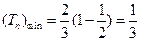 ---13分
---13分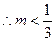 ,满足
,满足 的自然数为0,
的自然数为0,∴满足题设的自然数m存在,其值为0。 -------------------------14分

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
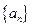 满足递推关系
满足递推关系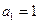 且
且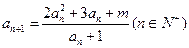 .
.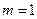 时,求数列
时,求数列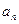 ;(2) 当
;(2) 当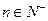 时,数列
时,数列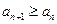 恒成立,求
恒成立,求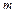 的取值范围;(3) 在
的取值范围;(3) 在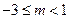 时,证明:
时,证明: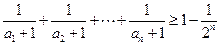 .
.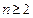 时,其前n项和满足
时,其前n项和满足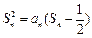
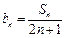 ,数列{bn}的前n项和为Tn,求Tn.
,数列{bn}的前n项和为Tn,求Tn.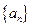 满足:
满足: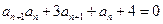
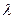 ,使得
,使得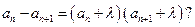 请对你的结论作出正确的解释或证明;
请对你的结论作出正确的解释或证明;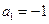 时,求数列
时,求数列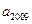 是数列
是数列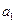 的取值范围。
的取值范围。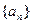 是等差数列,
是等差数列,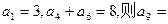 .
.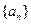 中,
中,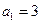 ,前
,前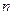 项和为
项和为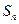 ,等比数列
,等比数列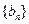 各项均为正数,
各项均为正数,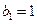 ,且
,且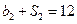 ,
,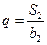
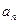 与
与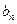 ;
;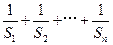
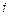 行第
行第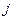 列的数为
列的数为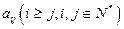 ,则
,则