题目内容
9.有下列四个命题,其中正确的命题有( )①A、B到α的距离相等,则AB∥α;
②△ABC的三个顶点到平面α的距离相等,则平面ABC∥α;
③夹在两个平行平面间的平行线段相等;
④垂直于同一个平面的两条直线互相平行.
| A. | ①② | B. | ②③ | C. | ③ | D. | ③④ |
分析 若A、B到α的距离相等,则AB∥α或AB的中点在平面α上,可判断①;
若△ABC的三个顶点到平面α的距离相等,则平面ABC∥α或△ABC的中位线?平面α,可判断②;
由面面平行的几何特征及性质,可判断③;
由线面垂直的性质定理,可判断④.
解答 解:①A、B到α的距离相等,则AB∥α或AB的中点在平面α上,故①错误;
②△ABC的三个顶点到平面α的距离相等,则平面ABC∥α或△ABC的中位线?平面α,故②错误;
③夹在两个平行平面间的平行线段相等,故③正确;
④垂直于同一个平面的两条直线互相平行,故④正确.
故正确的命题有:③④,
故选:D
点评 本题考查的知识点是命题的真假判断与应用,此类题型往往综合较多的其它知识点,综合性强,难度中档.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.下列判断中正确的是( )
| A. | 命题“?a∈R,a2+1≥2a”的否定是:“?a∈R,a2+1≤2a” | |
| B. | ?m∈R,使函数f(x)=(m-1)xm2-4m+1是幂函数,且在(0,+∞)上递减 | |
| C. | 命题“若a+$\frac{1}{a}$=2,则a=1”的逆否命题是假命题 | |
| D. | 已知直线l⊥平面α,直线m?平面β,则“α∥β”是“l⊥m”的充要条件 |
4.设x,y满足约束条件$\left\{\begin{array}{l}{x+y≥a}\\{x-y≤-1}\end{array}\right.$,且z=x+ay,则( )
| A. | 当a>0时有最大值 | B. | 当a>1时有最小值 | ||
| C. | 当a<0时有最大值 | D. | 当0<a<1时有最小值 |
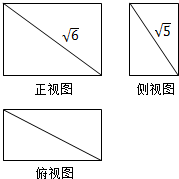 某长方体的三视图如图,长度为$\sqrt{10}$的体对角线在正视图中的长度为$\sqrt{6}$,在侧视图中的长度为$\sqrt{5}$,则该长方体的表面积为3+4$\sqrt{11}$.
某长方体的三视图如图,长度为$\sqrt{10}$的体对角线在正视图中的长度为$\sqrt{6}$,在侧视图中的长度为$\sqrt{5}$,则该长方体的表面积为3+4$\sqrt{11}$.