题目内容
设奇函数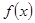 在
在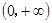 上为增函数,且
上为增函数,且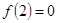 ,则不等式
,则不等式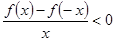 解集为( )
解集为( )
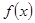 在
在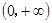 上为增函数,且
上为增函数,且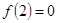 ,则不等式
,则不等式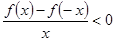 解集为( )
解集为( )A.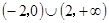 | B.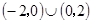 | C.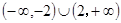 | D.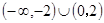 |
B
本试题主要是考查了抽象函数的单调性和解不等式的问题。
因为函数f(x)在(0,+∞)上为单调递减函数,且f(2)=0,∴函数f(x)在(0,2)的函数值为正,在(2,+∞)上的函数值为负,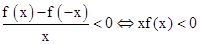
又奇函数f(x),所以有f(x)≥0,所以有0<x≤2,同理当x<0时,可解得-2≤x<0
故不等式的解集为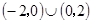 ,选B.
,选B.
解决该试题的关键是分析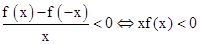 和函数的奇偶性,得到解集。
和函数的奇偶性,得到解集。
因为函数f(x)在(0,+∞)上为单调递减函数,且f(2)=0,∴函数f(x)在(0,2)的函数值为正,在(2,+∞)上的函数值为负,
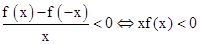
又奇函数f(x),所以有f(x)≥0,所以有0<x≤2,同理当x<0时,可解得-2≤x<0
故不等式的解集为
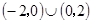 ,选B.
,选B.解决该试题的关键是分析
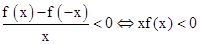 和函数的奇偶性,得到解集。
和函数的奇偶性,得到解集。
练习册系列答案
相关题目
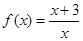 :
: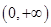 为单调递减函数;
为单调递减函数;  的奇偶性.
的奇偶性.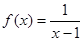 在(1,+∞)上是减函数.
在(1,+∞)上是减函数.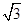 sinxcosx+2cos2x.
sinxcosx+2cos2x.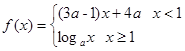 在
在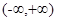 上是减函数,则
上是减函数,则 的取值范围为 .
的取值范围为 .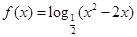 的单调递减区间为
的单调递减区间为 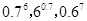 的大小关系为 ( )
的大小关系为 ( )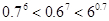
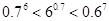
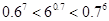
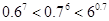
 的取值范围是( )
的取值范围是( )
 ∪(3,+∞)
∪(3,+∞)
 ∪(3,+∞)
∪(3,+∞)