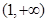题目内容
函数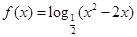 的单调递减区间为
的单调递减区间为
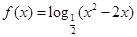 的单调递减区间为
的单调递减区间为 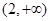
试题分析:首先令
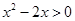 ,得
,得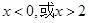 ,即函数的定义域为
,即函数的定义域为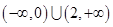 .又因为已知函数的底数为
.又因为已知函数的底数为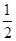 ,而
,而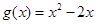 在
在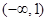 上单调递减,在
上单调递减,在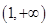 上单调递增,根据复合函数的单调性,知函数
上单调递增,根据复合函数的单调性,知函数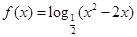 的单调递减区间为
的单调递减区间为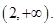 .
.点评:对于此类题目,学生应该准确分析组成复合函数的函数分别是什么,然后根据复合函数“同增异减”,判断函数的单调性及单调区间,另外需要特别注意的是要时刻注意函数的定义域,如果忽略定义域,很可能会出现错误的结论.

练习册系列答案
 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
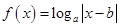 在
在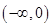 上是增函数,则
上是增函数,则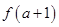 与
与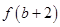 的
的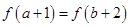
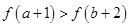
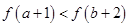
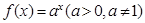 在
在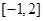 上的最大值为4,最小值为
上的最大值为4,最小值为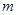 ,
,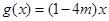 在R上是增函数,则
在R上是增函数,则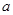 = .
= .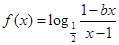 为奇函数,
为奇函数,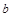 为常数.
为常数.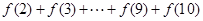 的值;
的值;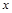 的值,不等式
的值,不等式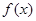 >
>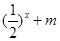 恒成立,求实数
恒成立,求实数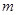 的取值范围.
的取值范围.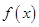 的定义域为A,若
的定义域为A,若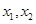
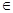 A,且
A,且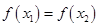 时总有
时总有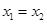 ,则称
,则称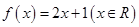 是单函数,下列命题:
是单函数,下列命题: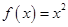
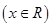 是单函数;
是单函数;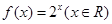 是单函数,
是单函数,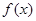 为单函数,
为单函数,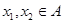 且
且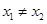 ,则
,则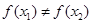 ;
;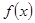 在
在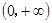 上为增函数,且
上为增函数,且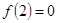 ,则不等式
,则不等式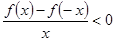 解集为( )
解集为( )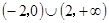
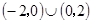
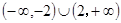
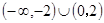
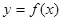 ,满足
,满足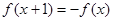 ,且在
,且在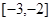 上是减函数,若
上是减函数,若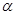 ,
,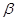 是锐角三角形的两个内角,则 ( )
是锐角三角形的两个内角,则 ( )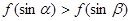


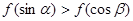
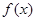 =
=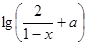 是奇函数,则
是奇函数,则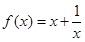 的单调递减区间是
的单调递减区间是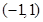
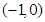
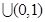
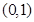
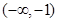 ,
,