题目内容
已知函数f(x)的定义域为[-3,+∞),且f(6)=2。f′(x)为f(x)的导函数,f′(x)的图象如图所示.若正数a,b满足f(2a+b)<2,则 的取值范围是( )
的取值范围是( )

 的取值范围是( )
的取值范围是( )
A. ∪(3,+∞) ∪(3,+∞) | B. |
C. ∪(3,+∞) ∪(3,+∞) | D. |
A
解:如图所示:f′(x)≥0在[-3,+∞)上恒成立∴函数f(x)在[-3,0)是减函数,(0,+∞)上是增函数,又∵f(2a+b)<2=f(6)
∴2a+b>0,2a+b<6,画出平面区域令t= ,表示过定点(2,-3)的直线的斜率,如图所示:t∈(-∞,-
,表示过定点(2,-3)的直线的斜率,如图所示:t∈(-∞,-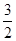 )∪(3,+∞)故选A
)∪(3,+∞)故选A
∴2a+b>0,2a+b<6,画出平面区域令t=
 ,表示过定点(2,-3)的直线的斜率,如图所示:t∈(-∞,-
,表示过定点(2,-3)的直线的斜率,如图所示:t∈(-∞,-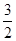 )∪(3,+∞)故选A
)∪(3,+∞)故选A
练习册系列答案
 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
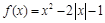 .(1)将函数
.(1)将函数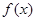 的解析式写成分段函数;
的解析式写成分段函数;
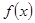 在
在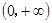 上为增函数,且
上为增函数,且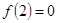 ,则不等式
,则不等式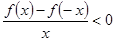 解集为( )
解集为( )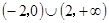
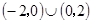
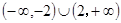
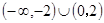
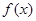 在
在 上有定义,对任意实数
上有定义,对任意实数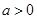 和任意实数
和任意实数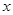 ,都有
,都有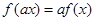 ,若
,若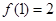 ,则函数
,则函数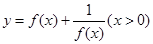 的递减区间是______.
的递减区间是______.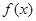 为减函数,且
为减函数,且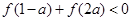 ,则
,则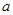 的取值范围
的取值范围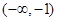
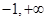 )
)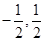 )
)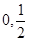 )
)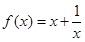 的单调递减区间是
的单调递减区间是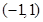
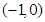
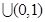
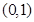
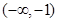 ,
,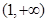
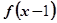 是偶函数,当
是偶函数,当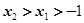 时,
时,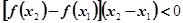 恒成立,设
恒成立,设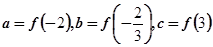 ,则a,b,c的大小关系( )
,则a,b,c的大小关系( )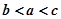
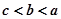
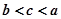
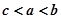
 的单调递减区间
的单调递减区间 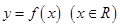 满足
满足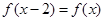 ,且
,且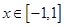 时,
时,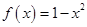
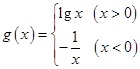 ,则函数
,则函数 在区间
在区间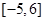 内的零点的个数为
内的零点的个数为