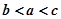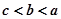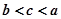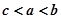题目内容
(12分)
用定义法证明:函数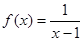 在(1,+∞)上是减函数.
在(1,+∞)上是减函数.
用定义法证明:函数
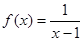 在(1,+∞)上是减函数.
在(1,+∞)上是减函数.见解析。
本小题利用单调性的定义证明第一步取值:设x1 ,x2是(1,+∞)上的任意两个实数,且x1<x2.第二步:作差变形再判断符号.即判断f(x1)- f(x2)的符号.
第三步得到结论.
证明:设x1 ,x2是(1,+∞)上的任意两个实数,且x1<x2,则 …….2分
f(x1)- f(x2)=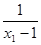 -
-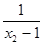 =
=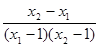 ……………6分
……………6分
∵x1 ,x2>1, ∴x1-1>0,x2-1>0
又∵x1<x2, ∴x2-x1>0 ………………………………….8分
∴f(x1)- f(x2)>0
即f(x1)>f(x2) ………………………………………………10分
所以,函数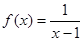 在(1,+∞)上是减函数. …………….12分
在(1,+∞)上是减函数. …………….12分
(作差,变形,再判断符号是必须的,否则要扣分.)
第三步得到结论.
证明:设x1 ,x2是(1,+∞)上的任意两个实数,且x1<x2,则 …….2分
f(x1)- f(x2)=
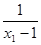 -
-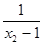 =
=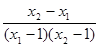 ……………6分
……………6分∵x1 ,x2>1, ∴x1-1>0,x2-1>0
又∵x1<x2, ∴x2-x1>0 ………………………………….8分
∴f(x1)- f(x2)>0
即f(x1)>f(x2) ………………………………………………10分
所以,函数
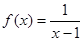 在(1,+∞)上是减函数. …………….12分
在(1,+∞)上是减函数. …………….12分(作差,变形,再判断符号是必须的,否则要扣分.)

练习册系列答案
相关题目
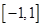 上的偶函数
上的偶函数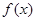 ,已知当
,已知当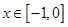 时的解析式
时的解析式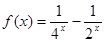
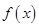 在
在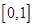 上的解析式;
上的解析式;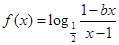 为奇函数,
为奇函数,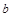 为常数.
为常数.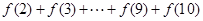 的值;
的值;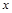 的值,不等式
的值,不等式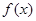 >
>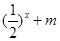 恒成立,求实数
恒成立,求实数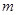 的取值范围.
的取值范围.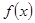 在
在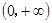 上为增函数,且
上为增函数,且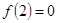 ,则不等式
,则不等式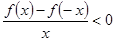 解集为( )
解集为( )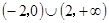
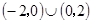
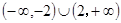
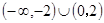
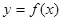 ,满足
,满足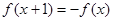 ,且在
,且在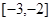 上是减函数,若
上是减函数,若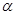 ,
,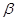 是锐角三角形的两个内角,则 ( )
是锐角三角形的两个内角,则 ( )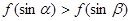


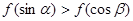
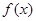 满足对一切
满足对一切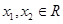 都有
都有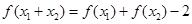 ,且
,且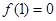 ,
,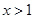 时有
时有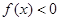 .
.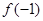 的值;
的值; 上的单调性;
上的单调性;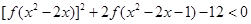 .
.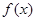 =
=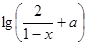 是奇函数,则
是奇函数,则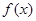 在
在 上有定义,对任意实数
上有定义,对任意实数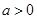 和任意实数
和任意实数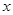 ,都有
,都有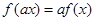 ,若
,若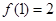 ,则函数
,则函数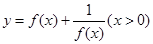 的递减区间是______.
的递减区间是______.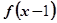 是偶函数,当
是偶函数,当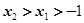 时,
时,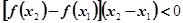 恒成立,设
恒成立,设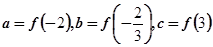 ,则a,b,c的大小关系( )
,则a,b,c的大小关系( )