题目内容
过椭圆 (
( )的左焦点
)的左焦点 作
作 轴的垂线交椭圆于点
轴的垂线交椭圆于点 ,
, 为右焦点,若
为右焦点,若 ,则椭圆的离心率为 ( )
,则椭圆的离心率为 ( )
A. | B. | C. | D. |
B
解析试题分析:由题意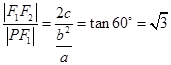 ,∴
,∴ ,∴
,∴ ,∴
,∴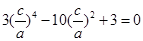 ,解得
,解得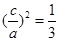 或3(舍去),故所求椭圆离心率e=
或3(舍去),故所求椭圆离心率e=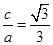 ,选B
,选B
考点:本题考查了椭圆离心率的求法
点评:若方程中的a,b,c没有直接给出,则应根据题意列出关于a,b,c的齐次方程,然后求解出离心率即可。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若直线mx- ny = 4与⊙O: x2+y2= 4没有交点,则过点P(m,n)的直线与椭圆 的交点个数是 ( )
的交点个数是 ( )
| A.至多为1 | B.2 | C.1 | D.0 |
已知F1,F2为双曲线C: 的左右焦点,点P在C上,
的左右焦点,点P在C上, ,则
,则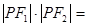 ( )
( )
| A. 2 | B. 4 | C. 6 | D. 8 |
已知椭圆 与双曲线
与双曲线 有相同的焦点
有相同的焦点 和
和 ,若
,若 是
是 的等比中项,
的等比中项,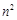 是
是 与
与 的等差中项,则椭圆的离心率是( )
的等差中项,则椭圆的离心率是( )
A. | B. | C. | D. |
当a为任意实数时,直线 恒过定点P,则过点P的抛物线的标准方程是( )
恒过定点P,则过点P的抛物线的标准方程是( )
A.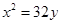 或 或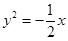 | B.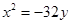 或 或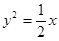 |
C.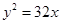 或 或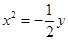  | D.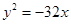 或 或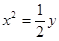 |
设 是椭圆
是椭圆 上的一点,
上的一点, 为焦点,且
为焦点,且 ,则
,则 的面积为( )
的面积为( )
A. | B. | C. | D.16 |
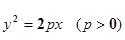 的焦点F恰好是双曲线
的焦点F恰好是双曲线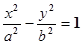 的右焦点,且两条曲线的交点的连线过F,则该双曲线的离心率为( )
的右焦点,且两条曲线的交点的连线过F,则该双曲线的离心率为( )
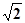

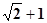
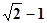
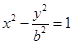 的左顶点A作斜率为1的直线
的左顶点A作斜率为1的直线 ,若
,若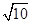 B.
B.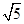 C.
C.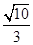 D.
D.
 的左焦点
的左焦点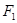 作斜率为1的直线,该直线与双曲线的两条渐近线的交点分别为A、B,若
作斜率为1的直线,该直线与双曲线的两条渐近线的交点分别为A、B,若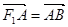 ,则双曲线的渐近线方程为( )
,则双曲线的渐近线方程为( )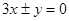 B.
B.
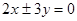 D.
D.