题目内容
【题目】如图,在直四棱柱ABCD﹣A1B1C1D1中,底面是边长为 ![]() 的正方形,AA1=3,点F在棱B1B上运动.
的正方形,AA1=3,点F在棱B1B上运动. 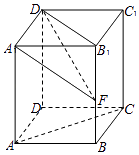
(1)若三棱锥B1﹣A1D1F的体积为 ![]() 时,求异面直线AD与D1F所成的角
时,求异面直线AD与D1F所成的角
(2)求异面直线AC与D1F所成的角.
【答案】
(1)解:∵在直四棱柱ABCD﹣A1B1C1D1中,底面是边长为 ![]() 的正方形,
的正方形,
∴ ![]() =
= ![]() =1,
=1,
∵AA1=3,点F在棱B1B上运动,三棱锥B1﹣A1D1F的体积为 ![]() ,
,
∴ ![]() ×B1F=
×B1F= ![]() =
= ![]() ,
,
∴BF=3﹣2=1,
以D为原点,DA为x轴,DC为y轴,
DD1为z轴,建立空间直角坐标系,
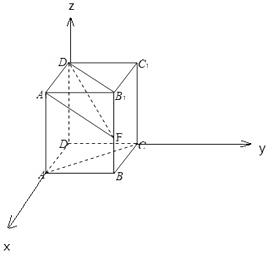
由A( ![]() ,0,0),D(0,0,0),
,0,0),D(0,0,0),
D1(0,0,3),F( ![]() ,
, ![]() ,1),
,1),
![]() =(﹣
=(﹣ ![]() ,0,0),
,0,0),
![]() =(
=( ![]() ,
, ![]() ,-2),
,-2),
设异面直线AD与D1F所成的角为θ,
则cosθ= 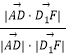 =
= ![]() =
= ![]() ,∴θ=60°.
,∴θ=60°.
∴异面直线AD与D1F所成的角为60°
(2)解:C(0, ![]() ,0),
,0), ![]() =(﹣
=(﹣ ![]() ,
, ![]() ,0),
,0), ![]() =(
=( ![]() ,
, ![]() ,-2),
,-2),
∵ ![]() =﹣2+2+0=0,
=﹣2+2+0=0,
∴异面直线AC与D1F所成的角为90°.
【解析】(1)求出BF=1,以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,利用向量法能求出异面直线AD与D1F所成的角.(2)求出 ![]() =(﹣
=(﹣ ![]() ,
, ![]() ,0),
,0), ![]() =(
=( ![]() ,
, ![]() ,-2),利用向量法能求出异面直线AC与D1F所成的角的大小.
,-2),利用向量法能求出异面直线AC与D1F所成的角的大小.
【考点精析】利用棱柱的结构特征和异面直线及其所成的角对题目进行判断即可得到答案,需要熟知两底面是对应边平行的全等多边形;侧面、对角面都是平行四边形;侧棱平行且相等;平行于底面的截面是与底面全等的多边形;异面直线所成角的求法:1、平移法:在异面直线中的一条直线中选择一特殊点,作另一条的平行线;2、补形法:把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体、长方体等,其目的在于容易发现两条异面直线间的关系.

 智慧小复习系列答案
智慧小复习系列答案