题目内容
【题目】若函数f（x）定义在R上的奇函数，且在（﹣∞，0）上是增函数，又f（2）=0，则不等式xf（x+1）＜0的解集为 ．
【答案】（0，1）∪（﹣3，﹣1）
【解析】解：∵函数f（x）定义在R上的奇函数，且在（﹣∞，0）上是增函数，又f（2）=0， ∴f（x）在（0，+∞）上是增函数，且f（﹣2）=﹣f（2）=0，
∴当x＞2或﹣2＜x＜0时，f（x）＞0，当x＜﹣2或0＜x＜2时，f（x）＜0，（如图）
则不等式xf（x+1）＜0等价为
或 
，
即 
或 
，
则 
或 
，
解得0＜x＜1或﹣3＜x＜﹣1，
故不等式的解集为（0，1）∪（﹣3，﹣1），
所以答案是：（0，1）∪（﹣3，﹣1）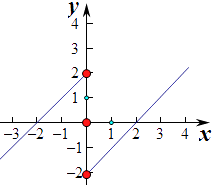
【考点精析】掌握奇偶性与单调性的综合是解答本题的根本，需要知道奇函数在关于原点对称的区间上有相同的单调性；偶函数在关于原点对称的区间上有相反的单调性．
练习册系列答案
相关题目
