题目内容
5.已知函数f(x)=$\frac{1}{3}$x3-a2x+$\frac{1}{2}$a(a∈R).(Ⅰ)当a=1时,函数g(x)=f(x)-b恰有3个零点,求实数b的取值范围;
(Ⅱ)若对任意x∈[0,+∞),有f(x)>0恒成立,求a的取值范围.
分析 (Ⅰ)求得a=1的函数f(x)的导数,求得单调区间和极值,由题意可得,只要b介于极小值和极大值之间;
(Ⅱ)求得f(x)的导数,对a讨论,当a=0时,当a>0时,当a<0时,求得单调区间,即可得到最小值,再由不等式恒成立思想即可得到.
解答 解:(Ⅰ)f'(x)=x2-1=(x+1)(x-1),
令f′(x)=0,x1=-1,x2=1,
当x变化时,f′(x),f(x)的取值情况如下:
| x | (-∞,-1) | -1 | (-1,1) | 1 | (1,+∞) |
| f′(x) | + | 0 | - | 0 | + |
| f(x) | 增 | 极大值 | 减 | 极小值 | 增 |
所以,实数b的取值范围是$(-\frac{1}{6},\frac{7}{6})$.
(Ⅱ)f′(x)=(x+a)(x-a),令f′(x)=0,x1=-a,x2=a,
(1)当a=0时,f(x)在[0,+∞)上为增函数,
∴f(x)min=f(0)=0不合题意;
(2)当a>0时,f(x)在(0,a)上是减函数,在(a,+∞)上为增函数,
∴f(x)min=f(a)>0,得$0<a<\frac{{\sqrt{3}}}{2}$;
(3)当a<0时,f(x)在(0,-a)上是减函数,在(-a,+∞)上为增函数,
∴f(x)min=f(-a)<f(0)<0,不合题意.
综上,$0<a<\frac{{\sqrt{3}}}{2}$.
点评 本题考查导数的运用:求单调区间和极值、最值,同时考查不等式恒成立思想转化为求函数的最值,注意运用分类讨论的思想方法,考查运算能力,属于中档题.

练习册系列答案
相关题目
16.已知tanα=$\frac{1}{7}$,tanβ=$\frac{1}{3}$,则tan(α+β)=( )
| A. | $\frac{1}{2}$ | B. | $\frac{5}{11}$ | C. | -$\frac{1}{5}$ | D. | -$\frac{2}{11}$ |
13.执行如图所示的程序框图,若“否”箭头分别指向①和②,则输出的结果分别是( )
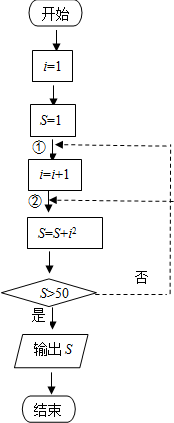

| A. | 55,53 | B. | 51,49 | C. | 55,49 | D. | 53,51 |
10.若双曲线$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1的渐近线方程是y=±$\sqrt{2}$x,则双曲线的离心率等于( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
17.函数f(x)=2lnx+$\frac{1}{x}$的单调递减区间是( )
| A. | (-∞,$\frac{1}{2}$] | B. | (0,$\frac{1}{2}$] | C. | [$\frac{1}{2}$,1) | D. | [1,+∞﹚ |
10.下列双曲线中,有一个焦点在抛物线y2=2x准线上的是( )
| A. | 6y2-12x2=1 | B. | 12x2-6y2=1 | C. | 2x2-2y2=1 | D. | 4x2-4y2=1 |