题目内容
15.某工厂年初用49万元购买一台新设备,第一年设备维修及原料消耗的总费用6万元,以后每年都增加2万元,新设备每年可给工厂创造收益25万元.(1)工厂第几年开始获利?
(2)若干年后,该工厂有两种处理该设备的方案:①年平均收益最大时,以14万元出售该设备;②总收益最大时,以9万元出售该设备.问出售该设备后,哪种方案年平均收益较大?
分析 (1)判断费用是以6为首项,2为公差的等差数列,设第n年时累计的纯收入为f(n).求出通项公式,利用f(n)>0,列出不等式,求解即可.
(2)方案①:列出年平均收入利用基本不等式求出最值;方案②:利用数列的函数的特征,通过二次函数求解最值即可.
解答 (本题满分16分)
解:(1)由题设,每年费用是以6为首项,2为公差的等差数列,
设第n年时累计的纯收入为f(n).
∴f(n)=25n-[6+8+…+(2n+4)]-49=-n2+20n-49,…(3分)
获利即为:f(n)>0∴-n2+20n-49>0,即n2-20n+49<0
⇒10-$\sqrt{51}$$<n<10+\sqrt{51}$,又n∈N,∴n=3,4,5,…,17. …6 分
∴当n=3时,即第3年开始获利;…(7分)
(2)方案①:年平均收入$\frac{f(n)}{n}=20-({n+\frac{49}{n}})≤20-14=6$(万元),此时n=7,
出售该设备后,年平均收益为$6+\frac{14}{7}=8$(万元);…11 分
方案②:f(n)=-(n-10)2+51,
∴当n=10时,f(n)max=51,
出售该设备后,年平均收益为$\frac{51+9}{10}=6$(万元),…15 分
故第一种方案年平均收益较大. …16 分
点评 本题考查数列与函数的综合应用,基本不等式求解最值,武承嗣的性质的应用,考查分析问题解决问题的能力.

练习册系列答案
相关题目
5.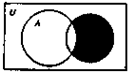 已知集合A={x∈Z||x|≤1},B={x|x2-2x=0},若全集U=R,则图中的阴影部分表示的集合为( )
已知集合A={x∈Z||x|≤1},B={x|x2-2x=0},若全集U=R,则图中的阴影部分表示的集合为( )
 已知集合A={x∈Z||x|≤1},B={x|x2-2x=0},若全集U=R,则图中的阴影部分表示的集合为( )
已知集合A={x∈Z||x|≤1},B={x|x2-2x=0},若全集U=R,则图中的阴影部分表示的集合为( )| A. | {-1} | B. | {2} | C. | {1,2} | D. | {0,2} |
6.阅读如图所示的程序框图,运行相应的程序,则输出的s的值为( )
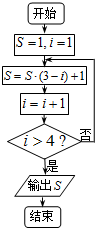

| A. | -1 | B. | 1 | C. | 0 | D. | 3 |
20.采用系统抽样的方法从2005个个体中抽取一个容量为50的样本,则抽样间隔和随机剔除的个体数分别为
( )
( )
| A. | 40,5 | B. | 50,5 | C. | 5,40 | D. | 5,50 |