题目内容
已知圆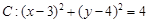 ,
,
(Ⅰ)若直线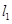 过定点
过定点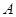 (1,0),且与圆
(1,0),且与圆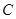 相切,求
相切,求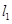 的方程;
的方程;
(Ⅱ) 若圆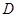 的半径为3,圆心在直线
的半径为3,圆心在直线 :
: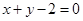 上,且与圆
上,且与圆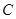 外切,求圆
外切,求圆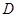 的方程.
的方程.
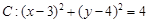 ,
,(Ⅰ)若直线
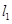 过定点
过定点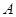 (1,0),且与圆
(1,0),且与圆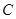 相切,求
相切,求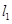 的方程;
的方程;(Ⅱ) 若圆
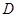 的半径为3,圆心在直线
的半径为3,圆心在直线 :
: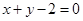 上,且与圆
上,且与圆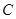 外切,求圆
外切,求圆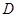 的方程.
的方程.(Ⅰ)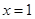 或
或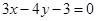 ; (Ⅱ)
; (Ⅱ) 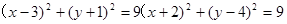
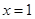 或
或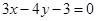 ; (Ⅱ)
; (Ⅱ) 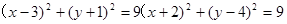
试题分析:(Ⅰ)此问注意直线斜率不存在的情况,应分斜率是否存在进行讨论,当斜率存在时由圆心到直线的距离等于半径求出直线斜率; (Ⅱ)先设出圆心坐标,然后由两圆外切,知圆心距等于两半径之和,从而求出圆心D的坐标,写出圆D方程.
试题解析:(Ⅰ)①若直线
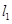 的斜率不存在,即直线是
的斜率不存在,即直线是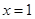 ,符合题意.
,符合题意.②若直线
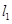 斜率存在,设直线
斜率存在,设直线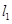 为
为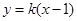 ,即
,即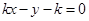 .
.由题意知,圆心(3,4)到已知直线
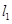 的距离等于半径2,
的距离等于半径2,即
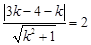 解之得
解之得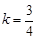 .所求直线方程是
.所求直线方程是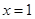 ,
,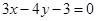 .
.(Ⅱ)依题意设
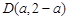 ,又已知圆的圆心
,又已知圆的圆心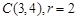 ,
,由两圆外切,可知
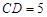
∴可知
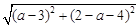 =
= ,解得
,解得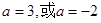 ,∴
,∴ 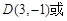
 ,
,∴所求圆的方程为
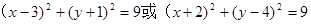 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
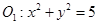 与⊙
与⊙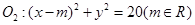 相交于
相交于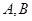 两点,且两圆在点
两点,且两圆在点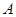 处的切线互相垂直,则线段
处的切线互相垂直,则线段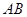 的长度是
的长度是 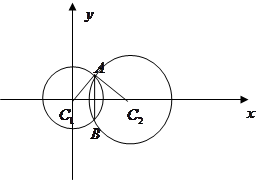
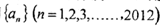 ,圆
,圆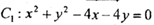 ,
,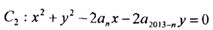 ,若圆C2平分圆C1的周长,则
,若圆C2平分圆C1的周长,则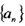 的所有项的和为.
的所有项的和为.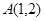 距离为1且与点
距离为1且与点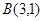 距离为2的直线共有 ( )
距离为2的直线共有 ( )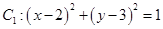 ,圆
,圆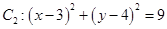 ,
,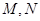 分别是圆
分别是圆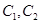 上的动点,
上的动点,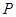 为
为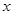 轴上的动点,则
轴上的动点,则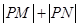 的最小值为( )
的最小值为( )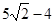
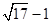
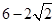
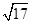
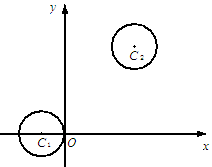
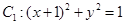 ,圆
,圆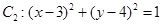 .
.
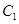 的直线
的直线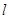 被圆
被圆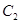 截得的弦长为
截得的弦长为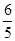 ,求直线
,求直线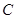 同时平分圆
同时平分圆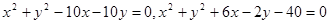 ,
,