题目内容
在平面直角坐标系xOy中，已知以O为圆心的圆与直线l：y=mx+（3-4m），（m∈R）恒有公共点，且要求使圆O的面积最小．
（1）写出圆O的方程；
（2）圆O与x轴相交于A、B两点，圆内动点P使|
|、|
|、|
|成等比数列，求
•
的范围；
（3）已知定点Q（-4，3），直线l与圆O交于M、N两点，试判断
•
×tan∠MQN是否有最大值，若存在求出最大值，并求出此时直线l的方程，若不存在，给出理由．
（1）写出圆O的方程；
（2）圆O与x轴相交于A、B两点，圆内动点P使|
| PA |
| PO |
| PB |
| PA |
| PB |
（3）已知定点Q（-4，3），直线l与圆O交于M、N两点，试判断
| QM |
| QN |
（1）因为直线l：y=mx+（3-4m）过定点T（4，3）
由题意，要使圆O的面积最小，定点T（4，3）在圆上，
所以圆O的方程为x2+y2=25．
（2）A（-5，0），B（5，0），设P（x0，y0），则x02+y02＜25 ①
=(-5-x0，-y0)，
=(5-x0，-y0)，
由|
|，|
|，|
|成等比数列得，|
|2=|
|•|
|，
即
+
=
•
，整理得：
-
=
，即
=
+
②
由①②得：0≤
＜
，
•
=(
-25)+
=2
-
，∴
•
∈[-
，0)
（3）
•
×tan∠MQN=|
|•|
|cos∠MQN×tan∠MQN
=|
|•|
|sin∠MQN=2S△MQN．
由题意，得直线l与圆O的一个交点为M（4，3），又知定点Q（-4，3），
直线lMQ：y=3，|MQ|=8，则当N（0，-5）时S△MQN有最大值32．
即
•
×tan∠MQN有最大值为64，
此时直线l的方程为2x-y-5=0．
由题意，要使圆O的面积最小，定点T（4，3）在圆上，
所以圆O的方程为x2+y2=25．
（2）A（-5，0），B（5，0），设P（x0，y0），则x02+y02＜25 ①
| PA |
| PB |
由|
| PA |
| PO |
| PB |
| PO |
| PA |
| PB |
即
| x | 20 |
| y | 20 |
(x0+5)2+
|
(x0-5)2+
|
| x | 20 |
| y | 20 |
| 25 |
| 2 |
| x | 20 |
| 25 |
| 2 |
| y | 20 |
由①②得：0≤
| y | 20 |
| 25 |
| 4 |
| PA |
| PB |
| x | 20 |
| y | 20 |
| y | 20 |
| 25 |
| 2 |
| PA |
| PB |
| 25 |
| 2 |
（3）
| QM |
| QN |
| QM |
| QN |
=|
| QM |
| QN |
由题意，得直线l与圆O的一个交点为M（4，3），又知定点Q（-4，3），
直线lMQ：y=3，|MQ|=8，则当N（0，-5）时S△MQN有最大值32．
即
| QM |
| QN |
此时直线l的方程为2x-y-5=0．
练习册系列答案
相关题目
，
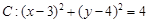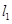过定点
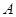(1，0)，且与圆
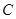相切，求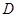
的半径为3，圆心在直线
：
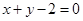上，且与圆