题目内容
若圆C1:x2+y2+2ax+a2-4=0(a∈R)与圆C2:x2+y2-2by+b2-1=0(b∈R)外切,则a+b的最大值为________.
3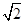 .
.
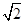 .
.依题意知C1:(x+a)2+y2=4,C2:x2+(y-b)2=1,则|C1C2|=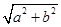 =2+1=3,∴a2+b2=9,∴
=2+1=3,∴a2+b2=9,∴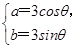 (θ为参数),
(θ为参数),
∴a+b=3(sin θ+cos θ)=3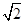 sin
sin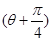 ≤3
≤3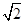 .
.
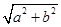 =2+1=3,∴a2+b2=9,∴
=2+1=3,∴a2+b2=9,∴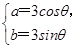 (θ为参数),
(θ为参数), ∴a+b=3(sin θ+cos θ)=3
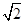 sin
sin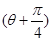 ≤3
≤3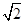 .
.
练习册系列答案
相关题目
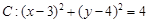 ,
,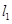 过定点
过定点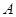 (1,0),且与圆
(1,0),且与圆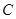 相切,求
相切,求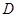 的半径为3,圆心在直线
的半径为3,圆心在直线 :
: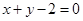 上,且与圆
上,且与圆 与圆
与圆 的公共弦长为
的公共弦长为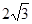 ,则
,则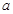 的值为
的值为

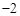
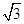 ,则a=________.
,则a=________.
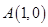 和点
和点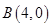 到直线
到直线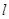 的距离依次为
的距离依次为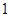 和
和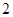 ,则这样的直线有( )
,则这样的直线有( )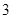 条
条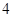 条
条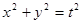 与圆
与圆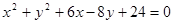 外切,则正数t的值是
外切,则正数t的值是