题目内容
15.已知函数f(x)=$\frac{{a}^{x}+1}{{a}^{x}-1}$(a>0,且a≠1).(1)求f(x)的定义域和值域;
(2)讨论f(x)的奇偶性;
(3)当a=2时,讨论函数f(x)的单调性,并用定义证明.
分析 (1)利用分母不为0,求出f(x)的定义域,f(x)=$\frac{{a}^{x}+1}{{a}^{x}-1}$=1+$\frac{2}{{a}^{x}-1}$,即可求出值域;
(2)利用奇偶性的定义,即可判断;
(3)任取x1,x2∈(0,+∞),且x1<x2,则f(x1)-f(x2)变形后易判>0,由单调性的定义可得.
解答 解:(1)由ax-1≠0,可得x≠0,∴f(x)的定义域是{x|x≠0};
f(x)=$\frac{{a}^{x}+1}{{a}^{x}-1}$=1+$\frac{2}{{a}^{x}-1}$∈(-∞,-1)∪(1,+∞).
(2)f(-x)=$\frac{{a}^{-x}+1}{{a}^{-x}-1}$=-$\frac{{a}^{x}+1}{{a}^{x}-1}$=-f(x),
∴f(x)是奇函数;
(3)a=2时,f(x)=1+$\frac{2}{{2}^{x}-1}$在(-∞,0),(0,+∞)上单调递减,
任取x1,x2∈(0,+∞),且x1<x2,则f(x1)-f(x2)=1+$\frac{2}{{2}^{{x}_{1}}-1}$-1-$\frac{2}{{2}^{{x}_{2}}-1}$
=$\frac{2({2}^{{x}_{2}}-{2}^{{x}_{1}})}{({2}^{{x}_{1}}-1)({2}^{{x}_{2}}-1)}$>0,
∴f(x)=1+$\frac{2}{{2}^{x}-1}$在(0,+∞)上单调递减.
点评 本题考查函数的单调性的判断与证明,考查函数的奇偶性、定义域和值域,属中档题.

练习册系列答案
相关题目
3.已知焦点在x轴上,长、短半轴之和为10,焦距为4$\sqrt{5}$,则椭圆的方程为( )
| A. | $\frac{{x}^{2}}{36}$+$\frac{{y}^{2}}{16}$=1 | B. | $\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{36}$=1 | C. | $\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{4}$=1 | D. | $\frac{{y}^{2}}{6}$+$\frac{{x}^{2}}{4}$=1 |
20.已知数列的通项公式an=n(n-3),则180是它的第( )项.
| A. | -12 | B. | -15 | C. | 12 | D. | 15 |
16.下列函数中,在区间(0,+∞)上是增函数的是( )
| A. | y=-x2+1 | B. | y=-2x+3 | C. | y=log3x | D. | $y={(\frac{1}{2})^x}$ |
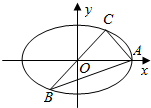 已知A、B、C是椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的三点,其中A的坐标为(2$\sqrt{3}$,0),BC过椭圆E的中心,且椭圆长轴的一个端点与短轴的两个端点构成正三角形.
已知A、B、C是椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的三点,其中A的坐标为(2$\sqrt{3}$,0),BC过椭圆E的中心,且椭圆长轴的一个端点与短轴的两个端点构成正三角形.