Question

7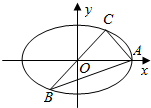．已知A、B、C是椭圆E：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的三点，其中A的坐标为（2$\sqrt{3}$，0），BC过椭圆E的中心，且椭圆长轴的一个端点与短轴的两个端点构成正三角形．
（1）求椭圆E的方程；
（2）当直线BC的斜率为1时，求△ABC面积；
（3）设直线l：y=kx+2与椭圆E交于两点P、Q，且线段PQ的中垂线过椭圆E与y轴负半轴的交点D，求实数k的值．

Answer 1

分析 （1）由题意可得a=2$\sqrt{3}$，再由正三角形的条件可得a=$\sqrt{3}$b，解得b，进而得到椭圆方程；
（2）由题意写出A点坐标，直线CB方程，联立直线方程与椭圆方程可求得交点C、B的纵坐标，S_△ABC=$\frac{1}{2}$|OA|•|y_B-y_C|，代入数值即可求得面积；
（3）联立直线l与椭圆方程消掉y得x的二次方程，设P（x₁，y₁），Q（x₂，y₂），线段PQ的中点H（x₀，y₀），由韦达定理及中点坐标公式可用k表示出中点坐标，由垂直可得k_DH•k_PQ=-1，解出即得k值，注意检验△＞0．

解答 解：（1）A的坐标为（2$\sqrt{3}$，0），即有a=2$\sqrt{3}$，
椭圆长轴的一个端点与短轴的两个端点构成正三角形，
可得a=$\sqrt{3}$b，解得b=2，
则椭圆E的方程为$\frac{{x}^{2}}{12}$+$\frac{{y}^{2}}{4}$=1；
（2）直线BC的方程为y=x，
代入椭圆方程x²+3y²=12，得y=x=±$\sqrt{3}$，
∴S_△ABC=$\frac{1}{2}$|OA|•|y_B-y_C|=$\sqrt{3}$×2$\sqrt{3}$=6；
（3）由$\left\{\begin{array}{l}{y=kx+2}\\{{x}^{2}+3{y}^{2}=12}\end{array}\right.$得（3k²+1）x²+12kx=0，△=（12k）²≥0，
依题意，k≠0，设P（x₁，y₁），Q（x₂，y₂），线段PQ的中点H（x₀，y₀），
则x₀=$\frac{{x}_{1}+{x}_{2}}{2}$，y₀=kx₀+2=$\frac{2}{1+3{k}^{2}}$，D（0，-2），H（-$\frac{6k}{1+3{k}^{2}}$，$\frac{2}{1+3{k}^{2}}$），
由k_DH•k_PQ=-1，得$\frac{\frac{2}{1+3{k}^{2}}+2}{-\frac{6k}{1+3{k}^{2}}}$=-$\frac{1}{k}$，解得k=±$\frac{\sqrt{3}}{3}$．
所以实数k的值为k=±$\frac{\sqrt{3}}{3}$．

点评 本题考查直线与椭圆的位置关系、三角形面积公式，韦达定理、判别式是解决该类题目的常用知识，要熟练掌握．