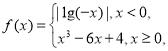题目内容
【题目】已知直线![]() 被圆
被圆![]() 所截得的弦长为8.
所截得的弦长为8.
(1)求圆![]() 的方程;
的方程;
(2)若直线![]() 与圆
与圆![]() 切于点
切于点![]() ,当直线
,当直线![]() 与
与![]() 轴正半轴,
轴正半轴,![]() 轴正半轴围成的三角形面积最小时,求点
轴正半轴围成的三角形面积最小时,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)利用点到直线的距离公式求出圆心到弦所在直线的距离,再利用弦长公式求出圆的半径即可求解;(2)设出直线和圆的切点,求出切点坐标和切线方程,求出切线方程和坐标轴的交点坐标,利用直角三角形的面积公式得到表达式,再利用基本不等式求其最值.
试题解析:(1)因为圆![]() 的圆心到直线
的圆心到直线![]() 的距离为
的距离为![]() ,………………1分
,………………1分
所以![]() .………………2分
.………………2分
所以圆![]() 的方程
的方程![]() .………………3分
.………………3分
(2)设直线![]() 与圆
与圆![]() 切于点
切于点![]() ,
,
则![]() .………………4分
.………………4分
因为![]() ,所以圆的切线的斜率为
,所以圆的切线的斜率为![]() .………………5分
.………………5分
则切线方程为![]() ,即
,即![]() .………………6分
.………………6分
则直线![]() 与
与![]() 轴正半轴的交点坐标为
轴正半轴的交点坐标为![]() ,与
,与![]() 轴正半轴的交点坐标为
轴正半轴的交点坐标为![]() .
.
所以围成的三角形面积为![]() .………………9分
.………………9分
因为![]() ,所以
,所以![]() .
.
当且仅当![]() 时,等号成立.………………10分
时,等号成立.………………10分
因为![]() ,
,![]() ,所以
,所以![]() ,
,
所以![]() .
.
所以当![]() 时,
时,![]() 取得最小值18.………………11分
取得最小值18.………………11分
所以所求切点![]() 的坐标为
的坐标为![]() .………………12分
.………………12分

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案
相关题目